剑指offer

剑指offer算法集。

最多能喝多少啤酒

题目：假如每3个空啤酒瓶可以换一瓶啤酒，某人买了10瓶啤酒，那么他最多可以喝到多少瓶啤酒？

答案：

1.如果能借酒瓶的话：15

喝完10瓶后用9个空瓶换来3瓶啤酒(喝完后有4个空瓶）喝完这三瓶又可以换到1瓶啤酒（喝完后有2个空瓶），这时他有2个空酒瓶，如果他能向老板先借一个空酒瓶，就凑够了3个空瓶可以换到一瓶啤酒，把这瓶喝完后将空瓶还给老板就可以了。所以他最多可以喝10+3+1+1=15瓶。

2.否则，14

如何倒出2两酒

据说有人给酒肆的老板娘出了一个难题：此人明明知道店里只有两个舀酒的勺子，分别能舀7两和11两酒，却硬要老板娘卖给他2两酒。聪明的老板娘毫不含糊，用这两个勺子在酒缸里舀酒，并倒来倒去，居然量出了2两酒，聪明的你能做到吗？

答案： 11,0–>4,7–>4,0–>0,4–>11,4–>8,7–>8,0–>1,7–>1,0–>0,1–>11,1–>5,7–>5,0–>0,5–>11,5–>9,7–>9,0–>2,7，这样就有2两了。

必胜策略

考虑一个双人游戏。游戏在一个圆桌上进行。每个游戏者都有足够多的硬币。他们需要在桌子上轮流放置硬币，每次必需且只能放置一枚硬币，要求硬币完全置于桌面内（不能有一部分悬在桌子外面），并且不能与原来放过的硬币重叠。谁没有地方放置新的硬币，谁就输了。游戏的先行者还是后行者有必胜策略？这种策略是什么？

答案：先行者在桌子中心放置一枚硬币，以后的硬币总是放在与后行者刚才放的地方相对称的位置。这样，只要后行者能放，先行者一定也有地方放。先行者必胜。

为什么多了一块

答案：剩余的和总价之间没有关系

移动火柴

答案：下面是各种各样的答案

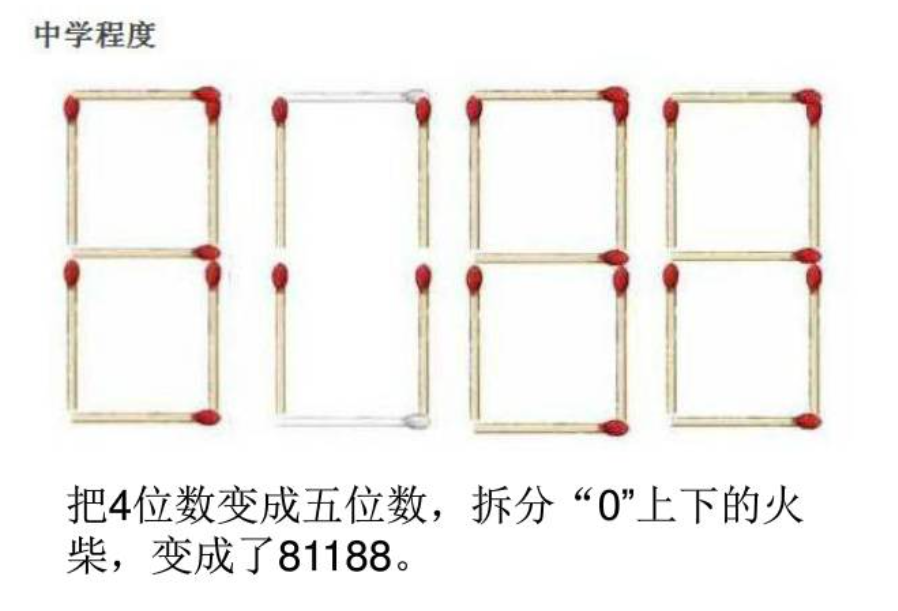
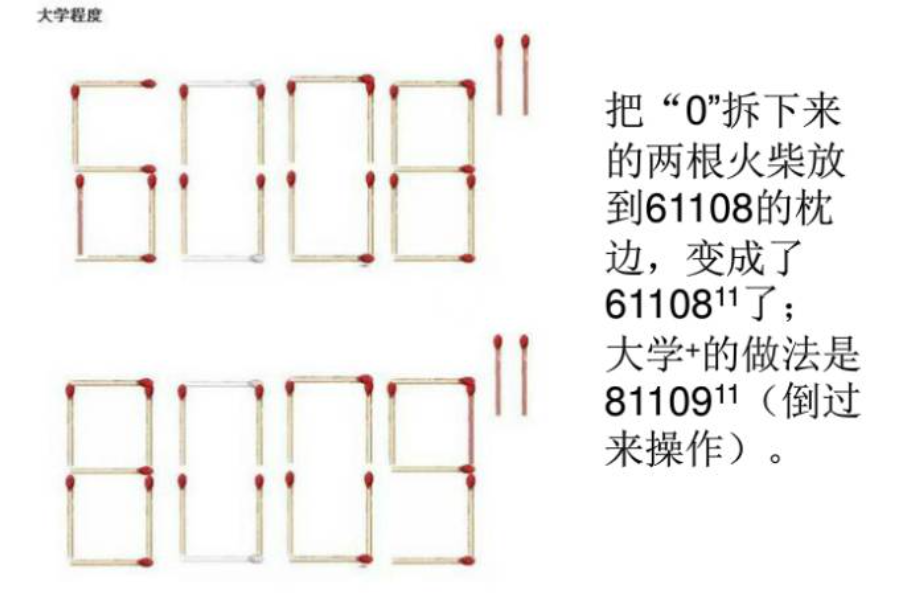
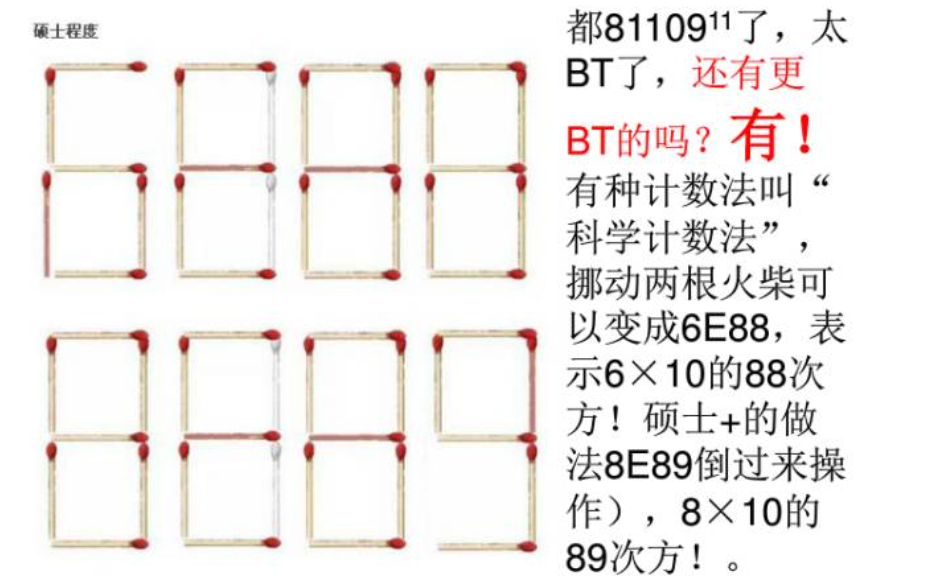
灯管问题

在房里有三盏灯，房外有三个开关，在房外看不见房内的情况，你只能进门一次，你用什么方法来区分那个开关控制那一盏灯？

答案：先打开第一个开关，开一会再关上，然后打开第二个开关进入房间再摸一下每个灯，发热的那盏是第一个开关的，亮的那盏是第二个开关的，没变化的那盏是第三个开关的 。

10人电梯

　题目：回答前请先仔细把问题看十遍！并逐字推敲！电梯最多能乘坐10人，你正好是第10个，走进电梯后却超重了，你只好走出电梯，电梯门关上后，你想到了一件恐怖的事情，立即报警。请问，怎么回事？
　　提示：回答之前，请先仔细把这些提示看三遍！
　　提示1：当时是夏天，电梯里9人有男有女，没有孕妇，没有胖子，没有宠物。没有人穿厚衣服。没有裙下藏人。
　　提示2：电梯没坏。顶部底部都没有藏尸体。9个人没有分食。电梯里面没有镜子。进来的人不是电梯修理工也不是凶手。广告里也没有人脸。没有鬼，没有超自然力量。
　　提示3：没有人携带拉杆箱之类可抛尸的包裹物。
　　提示4：不要去网络搜索，网上所有答案都不对。
　　提示5：请仔细多看几遍题目，答案就隐藏在题目.里面。没有其他的假设和设定，没有其他的前提条件。答案就藏在题目里。全部信息都已经呈现出来了。答案就在题目之内，请多看几遍，逐字逐句推敲。你需要超强的逻辑力和想象力，才能发现答案！
　　提示6：要有逻辑力，还要有想象力。得到这个道题的答案需要：超级逻辑力+超级想象力。
　　提示7：答案绝对恐怖，绝对变态！绝对不是常规思维能想的出来的！让你的变态想象力燃烧吧！
　　提示8：这道题有唯一的标准答案。不脑筋急转弯，不天马行空。答案很唯一，很标准。最终我会公布。答案绝对在常理之外，情理之中。经过艰难的思索，得到答案之后，你绝对会恍然大悟，就像吸食了吗啡一样爽！
　　提示9：请别往复杂里想。答案很简单。就摆在题目里。答案就一句话。这一句话绝对震撼+ 刺激 +超常 +恐怖 +变态 ！

答案：

【案情推理分析】：此案的关键就是找出电梯超重的理由以及当事人报警的原因。灵异事件，机械故障，当事人的精神问题排除在外一个十人承载的电梯之所以在走进第十个人会超载，是因为所谓的第十人实际上是第十一人，也就是说，在看似只有9人的电梯里，已经有了十个人，所以导致当事人走进电梯时候发现已经超载根据题目所说的“电梯顶部没有尸体”，则说明被隐藏的第十一人已经死亡，尸体被隐藏。而尸体被隐藏在电梯里的原因，则是因为电梯内的9人是共犯。有人说是9人分尸藏在身上，也有人是分食尸体，不但恶心没有艺术感，而且也不符合命题。命题的目的已经很明显，不可能藏尸。既然如此，那么我们就可以初步确定，尸体在电梯内，并且被巧妙隐藏。有了以上这点根据，我们在看第二个关键：当事人如何发现异常由命题可以看到，当事人走进了电梯，发现超重后走了出来，在关上电梯门后，“感觉”恐怖，才报案在这里，“感觉”两个字看似平常，却意义重大。在关门后才感觉到的异常，说明并非由直接感官造成，不是声音，不是气味，所以这也更加否定了分尸分食说。那么，为什么要在关门后才会感觉到？说明电梯关门的过程让他察觉到了异样。“电梯关门后”也许提示的是时间，也可能提示的是“感觉”触发的起点。提示时间并没有意义，那么就是提示“感觉恐怖”的触发起点。综上所述，电梯内巧妙掩藏着尸体，并且不能被感官察觉，但是在电梯关门的时候会发现异常。坐过电梯的人都知道，电梯的门是从两边往中间关上的，也就是说，在电梯外的人往电梯内看时，视野被一点点压缩，最后停留在中间那一条上。而中间那一条，则一般是广告画或者是镜子。那么我们再次来整理一下：当事人进入电梯，没有察觉异样，但是出了电梯，随着电梯门关上发现了异常并且报了警，说明藏尸方式跟广告画有关。推理到这里应该结束了，接下来是艺术渲染发挥假设的时候了为了让大家感受直接，写成一个情景重现小故事比较带感 【情景重现】这天，当事人等待电梯，电梯门打开，当事人进入电梯，发现已经超载，但是电梯里只有九人，在其他九人不耐烦的注视下，他一边纳闷一边讪讪退出了电梯，抱怨着等待下一班电梯。随着电梯门慢慢的关上，他的视野逐渐被缩小，最后停留在众人肩膀后那幅广告画上。那幅广告画，是他最喜欢的女明星的一副美白肌肤化妆品的广告画，里面她是那么的美丽，总是带着一缕浅浅的微笑。只是。。。。今天，广告画里的她没有微笑！！！他突然明白了什么，疯狂的拨打电话报警！事实上，广告画里的女明星已经被这九人杀害，脸色惨白，那九人想把尸体带到地下停车场带走，但是又怕监控发现尸体，于是扶着已经变僵的女尸乘坐电梯。之所以让其在生前的广告画前，是由于人进入电梯的第一视野很杂乱，不习惯直视众人，且习惯面对电梯门，转身而立，不知道身后站立着一具尸体。当事人进去也不例外，习以为常转身，并没有发现异常。而出了电梯门，随着电梯门的关闭，当事人的视野随即发生聚焦，发现了肩膀后面女尸的惨白的脸！

人民币为何只有1、2、5、10四种面值

题目：人民币为什么只有1、2、5、10的面值？忽略大于10的50,100神马的，那不是重点。另外，为什么2元人民币消失了呢？

用1.2.5.10就能以最少的加减组成另一些数,如1+2=3 2+2=4.1+5=6.2+5=7.10-2=8.10-1=9 如果将这四个’重要数’ 中的任何一个数用’非重要数’代替,就会出现有的数要两次以上 的加减才能组成另一些数的繁琐现象.更多详见：人民币为何只有1、2、5、10四种面值。

另外，既然1 2 5 10 是“重要数”，为何2元的人民币变得越来越少？

​ 中国人民银行在1999年7月1日发行第五套人民币时就明确了100元、50元、20元、10元、5元、1元、5角和1角八个券种，并根据优化币种的原则，停止发行2元和2角这两个券种。
　　随着国家经济发展，物价也跟着上涨，人民币发行的面额随之变化，导致10元人民币的使用率进一步提高，成为货币流通交易主体，2元人民币使用的频率进一步降低。为了节约印刷和制版费用，同时使人民币面额结构更加合理，中国人民银行才决定停止发行。据此，1999年6月30日国务院第268号令，决定取消2元人民币发行，2元人民币逐渐淡出了货币流通领域。
　　虽然第四套人民币目前还在流通，但从2004年开始，人民银行就宣布对2元采取“只收不付”的政策，而新发行的第五套人民币又取消了这个券种，所以，2元在市场上越来越少，仅在等待人民银行宣布退出流通。

概率悖论

弦长大于的概率？

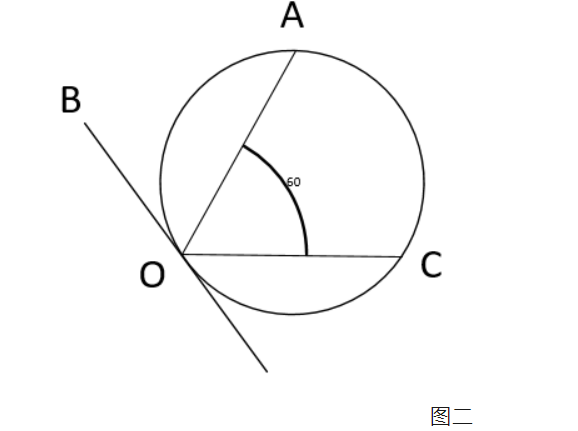
如图一，在半径为1的单位圆中，<AOB为120度，我们容易知道，弦AB的长度是。问题：任意一个弦长，长度大于的概率？下面有三种答案：

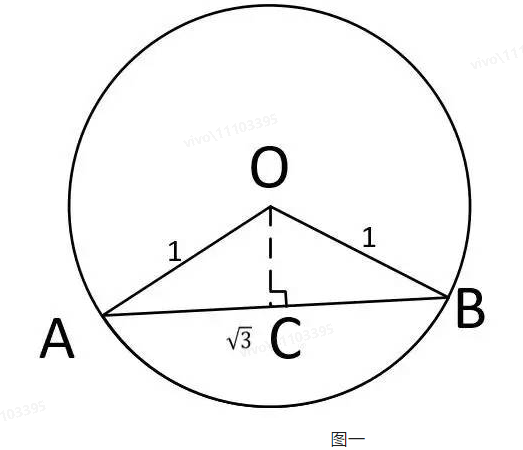
答案一：

​ 如图二，<AOC为60度，其角平分线过原点，因此，AO=OC=。任意一条过O的直线，如果在<AOC范围内，则弦长大于。否则，小于。因此，概率为角度之比=60/180=1/3.

答案二：

​ 如图三，任意一条弦，CAD，半径OB垂直于弦，如图所示。其中A为OB的中点，我们知道，如果CAD与OA相交，则长度大于，否则小于。因此，概率为1/2.

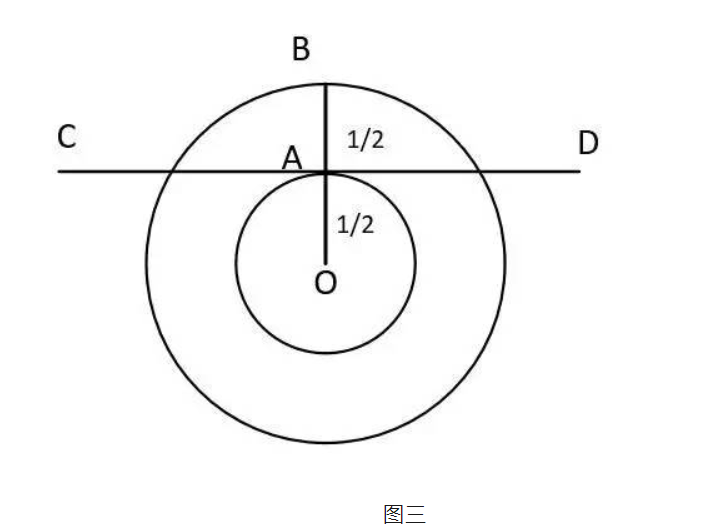
答案三：

​ 如图三，AO为半径1/2的圆。OB为单位圆。如果直线CD与圆OA相交，则长度大于，因此，概率为面积的比值：1/4.

考虑一个内接于圆的等边三角形。若随机选方圆上的个弦，则此弦的长度比三角形的边较长的机率为何？

在一给定圆内所有的弦中任选一条弦，求该弦的长度长于圆的内接正三角形边长的概率。该问题如图一，有三种解决方法。

1．如图1第一幅图，在垂直于三角形任意一边的直径上随机取一个点，并通过该点做一条垂直于该直径的弦，由圆内接正三角形的性质可得，在该点位于半径中点的时候弦长度等于三角形的边长度，当点离圆心的距离小于 时弦长度大于三角形边长。所以概率

2．如图1第二幅图，通过三角形任意一个顶点做圆的切线，因为等边三角形内角为60°，所以左边右边的角都是60°。由该顶点做一条弦，弦的另一端在圆上任意一点。由图可知弦与切线成60°角和120°角之间的时候弦长度大于三角形边长。所以概率

3．如图1第三幅图，当弦的中点在阴影标记的圆内时，弦的长度大于三角形的边长，而大圆的弦中点一定在圆内，大圆的面积是 ，小圆的面积是 。所以概率 。

答案解析：

解法一：由于对称性，可预先指定弦的方向。作垂直于此方向的直径，只有交直径于1/4 点与 3/4 点间的弦，其长才大于内接正三角形边长。所有交点是等可能的,则所求概率为1/2 。此时假定弦的中心在直径上均匀分布。

解法二：由于对称性，可预先固定弦的一端。仅当弦与过此端点的切线的交角在60°～ 120° 之间，其长才合乎要求。所有方向是等可能的，则所求概率为1/3 。此时假定端点在圆周上均匀分布。

解法三： 弦被其中点位置唯一确定。只有当弦的中点落在半径缩小了一半的同心圆内，其长才合乎要求。中点位置都是等可能的,则所求概率为1/4。此时假定弦长被其中心唯一确定。

这导致同一事件有不同概率，因此为悖论。

同一问题有三种不同答案，究其原因在于圆内“取弦”时规定尚不够具体，不同的“等可能性假定”导致了不同的样本空间，具体如下：其中“均匀分布”应理解为“等可能取点”。

解法一中假定弦的中点在直径上均匀分布，直径上的点组成样本空间Ω1.

解法二中假定弦的另一端在圆周上均匀分布，圆周上的点组成样本空间Ω2.

解法三中假定弦的中点在大圆内均匀分布，大圆内的点组成样本空间Ω3.

可见，上述三个答案是针对三个不同样本空间引起的，它们都是正确的，贝特朗悖论引起人们注意，在定义概率时要事先明确指出样本空间是什么。

猜牌游戏

S 先生、P先生、Q先生他们知道桌子的抽屉里有16张扑克牌：红桃A、Q、4 黑桃J、8、4、2、7、3 草花K、Q、5、4、6 方块A、5。约翰教授从这16张牌中挑出一张牌来，并把这张牌的点数告诉 P先生，把这张牌的花色告诉Q先生。这时，约翰教授问P先生和Q 先生：你们能从已知的点数或花色中推知这张牌是什么牌吗？ 于是，S先生听到如下的对话：
P先生：我不知道这张牌。
Q先生：我知道你不知道这张牌。
P先生：现在我知道这张牌了。
Q先生：我也知道了。
听罢以上的对话，S先生想了一想之后，就正确地推出这张牌是什么牌。
请问：这张牌是什么牌？

解释：

P第一句表明点数为A,Q,5,4其中一种
Q第一句表明花色为红桃或方块
P第二句表明不是A
Q第二句表明只能是方块5
答案：方块5

猜数游戏

题目：

已知两个1~30之间的数字，甲知道两数之和，乙知道两数之积。
甲问乙：”你知道是哪两个数吗？”乙说：”不知道”；
乙问甲：”你知道是哪两个数吗？”甲说：”也不知道”；
于是，乙说：”那我知道了”；
随后甲也说：”那我也知道了”；
这两个数是什么？

• 允许两数重复的情况下

答案：x=1，y=4；甲知道和A=x+y=5，乙知道积B=x*y=4

• 不允许两数重复的情况下有两种答案
  答案1：为x=1，y=6；甲知道和A=x+y=7，乙知道积B=x*y=6
  答案2：为x=1，y=8；甲知道和A=x+y=9，乙知道积B=x*y=8

解：
设这两个数为x，y.
甲知道两数之和 A=x+y；
乙知道两数之积 B=x*y；
该题分两种情况 ：
允许重复， 有(1 <= x <= y <= 30)；
不允许重复，有(1 <= x < y <= 30)；

*当不允许重复，即(1 <= x < y <= 30)**
1)由题设条件：乙不知道答案
<=> B=x*y 解不唯一
=> B=x*y 为非质数
又∵ x ≠ y
∴ B ≠ k*k (其中k∈N)
结论(推论1)：
B=x*y 非质数且 B ≠ k*k (其中k∈N)
即：B ∈(6，8，10，12，14，15，18，20…)
证明过程略。
2)由题设条件：甲不知道答案
<=> A=x+y 解不唯一
=> A >= 5；
分两种情况：
A=5，A=6时x，y有双解
A>=7 时x，y有三重及三重以上解
假设 A=x+y=5
则有双解
x1=1，y1=4；
x2=2，y2=3
代入公式B=x*y：
B1=x1*y1=1*4=4；(不满足推论1，舍去)
B2=x2*y2=2*3=6；
得到唯一解x=2，y=3即甲知道答案。
与题设条件：”甲不知道答案”相矛盾 ，
故假设不成立，A=x+y≠5
假设 A=x+y=6
则有双解。
x1=1，y1=5；
x2=2，y2=4
代入公式B=x*y：
B1=x1*y1=1*5=5；(不满足推论1，舍去)
B2=x2*y2=2*4=8；
得到唯一解x=2，y=4
即甲知道答案
与题设条件：”甲不知道答案”相矛盾
故假设不成立，A=x+y≠6
当A>=7时
∵ x，y的解至少存在两种满足推论1的解
B1=x1*y1=2*(A-2)
B2=x2*y2=3*(A-3)
∴ 符合条件
结论(推论2)：A >= 7
3)由题设条件：乙说”那我知道了”
=>乙通过已知条件B=x*y及推论(1)(2)可以得出唯一解
即：
A=x+y， A >= 7
B=xy， B ∈(6，8，10，12，14，15，16，18，20…)
1 <= x < y <= 30
x，y存在唯一解
当 B=6 时：有两组解
x1=1，y1=6
x2=2，y2=3 (∵ x2+y2=2+3=5 < 7∴不合题意，舍去)
得到唯一解 x=1，y=6
当 B=8 时：有两组解
x1=1，y1=8
x2=2，y2=4 (∵ x2+y2=2+4=6 < 7∴不合题意，舍去)
得到唯一解 x=1，y=8
当 B>8 时：容易证明均为多重解
结论：
当B=6时有唯一解 x=1，y=6；当B=8时有唯一解 x=1，y=8

4)由题设条件：甲说”那我也知道了”
=> 甲通过已知条件A=x+y及推论(3)可以得出唯一解
综上所述，原题所求有两组解：
x1=1，y1=6
x2=1，y2=8

当x<=y时，有(1 <= x <= y <= 30)：
同理可得唯一解 x=1，y=4

相遇问题

两个机器人，初始时位于数轴上的不同位置。给这两个机器人输入一段相同的程序，使得这两个机器人保证可以相遇。程序只能包含“左移n个单位”、“右移n个单位”，条件判断语句If，循环语句while，以及两个返回Boolean值的函数“在自己的起点处”和“在对方的起点处”。你不能使用其它的变量和计数器。

答案：两个机器人同时开始以单位速度右移，直到一个机器人走到另外一个机器人的起点处。然后，该机器人以双倍速度追赶对方。程序如下。

while(!at_other_robots_start) { 
  move_right 1 
} 
while(true) { 
  move_right 2 
}

找点问题

地球上有哪些点，使得从该点出发向南走一英里，向东走一英里，再向北走一英里之后恰好回到了起点？

答案：“北极点”是一个传统的答案，其实这个问题还有其它的答案。事实上，满足要求的点有无穷多个。所有距离南极点1 + 1/(2π)英里的地方都是满足要求的，向南走一英里后到达距离南极点1/(2π)的地方，向东走一英里后正好绕行纬度圈一周，再向北走原路返回到起点。事实上，这仍然不是满足要求的全部点。距离南极点1 + 1/(2kπ)的地方都是可以的，其中k可以是任意一个正整数。

握手问题

一对夫妇邀请N-1对夫妇参加聚会（因此聚会上总共有2N人）。每个人都和所有自己不认识的人握了一次手。然后，男主人问其余所有人（共2N-1个人）各自都握了几次手，得到的答案全部都不一样。假设每个人都认识自己的配偶，那么女主人握了几次手？

一对夫妇邀请N-1对夫妇参加聚会（因此聚会上总共有2N人）。每个人都和所有自己不认识的人握了一次手。然后，男主人问其余所有人（共2N-1个人）各自都握了几次手，得到的答案全部都不一样。假设每个人都认识自己的配偶，那么女主人握了几次手？

答案：握手次数只可能是从0到2N-2这2N-1个数。除去男主人外，一共有2N-1个人，因此每个数恰好出现了一次。其中有一个人(0)没有握手，有一个人(2N-2)和所有其它的夫妇都握了手。这两个人肯定是一对夫妻，否则后者将和前者握手（从而前者的握手次数不再是0）。除去这对夫妻外，有一个人(1)只与(2N-2)握过手，有一个人(2N-3)和除了(0)以外的其它夫妇都握了手。这两个人肯定是一对夫妻，否则后者将和前者握手（从而前者的握手次数不再是1）。以此类推，直到握过N-2次手的人和握过N次手的人配成一对。此时，除了男主人及其配偶以外，其余所有人都已经配对。根据排除法，最后剩下来的那个握手次数为N-1的人就是女主人了。

识别好坏处理器

你在一个飞船上，飞船上的计算机有n个处理器。突然，飞船受到外星激光武器的攻击，一些处理器被损坏了。你知道有超过一半的处理器仍然是好的。你可以向一个处理器询问另一个处理器是好的还是坏的。一个好的处理器总是说真话，一个坏的处理器总是说假话。用n-2次询问找出一个好的处理器。

答案：你在一个飞船上，飞船上的计算机有n个处理器。突然，飞船受到外星激光武器的攻击，一些处理器被损坏了。你知道有超过一半的处理器仍然是好的。你可以向一个处理器询问另一个处理器是好的还是坏的。一个好的处理器总是说真话，一个坏的处理器总是说假话。用n-2次询问找出一个好的处理器。

答案：给处理器从1到n标号。用符号a->b表示向标号为a的处理器询问处理器b是不是好的。首先问1->2，如果1说不是，就把他们俩都去掉（去掉了一个好的和一个坏的，则剩下的处理器中好的仍然过半），然后从3->4开始继续发问。如果1说2是好的，就继续问2->3，3->4，……直到某一次j说j+1是坏的，把j和j+1去掉，然后问j-1 -> j+2；或者从j+2 -> j+3开始发问，如果前面已经没有j-1了（之前已经被去掉过了）。注意到你始终维护着这样一个“链”，前面的每一个处理器都说后面那个是好的。这条链里的所有处理器要么都是好的，要么都是坏的。当这条链越来越长，剩下的处理器越来越少时，总有一个时候这条链超过了剩下的处理器的一半，此时可以肯定这条链里的所有处理器都是好的。或者，越来越多的处理器都被去掉了，链的长度依旧为0，而最后只剩下一个或两个处理器没被问过，那他们一定就是好的了。另外注意到，第一个处理器的好坏从来没被问过，仔细想想你会发现最后一个处理器的好坏也不可能被问到（一旦链长超过剩余处理器的一半，或者最后没被去掉的就只剩这一个了时，你就不问了），因此询问次数不会超过n-2。

乒乓球问题

假设排列着100个乒乓球，由两个人轮流拿球装入口袋，能拿到第100个乒乓球的人为胜利者。条件是：每次拿球者至少要拿1个，但最多不能超过5个，问：如果你是最先拿球的人，你该拿几个？以后怎么拿就能保证你能得到第100个乒乓球？

答案：先拿4个。

然后对方如果拿1到5个我就拿5到1个。于是无论如何剩下的球数为6n，n逐次少1，最后剩6个的时候恰好是我拿完，此时必胜。

如何分金条

你让工人为你工作7天，给工人的回报是一根金条。金条平分成相连的7段，你必须在每天结束时给他们一段金条，如果只许你两次把金条弄断，你如何给你的工人付费？

答案：把金条分为1，2，4，有点儿像我们的纸币只需要1，2，5就能对付所有的找钱问题！

猜数游戏

一个教授逻辑学的教授，有三个学生，而且三个学生均非常聪明！一天教授给他们出了一个题，教授在每个人脑门上贴了一张纸条并告诉他们，每个人的纸条上都写了一个正整数，且某两个数的和等于第三个！（每个人可以看见另两个数，但看不见自己的）教授问第一个学生：你能猜出自己的数吗？回答：不能，问第二个，不能，第三个，不能，再问第一个，不能，第二个，不能，第三个：我猜出来了，是144！教授很满意的笑了。请问您能猜出另外两个人的数吗？

答案：
经过第一轮，说明任何两个数都是不同的。第二轮，前两个人没有猜出，说明任何一个数都不是其它数的两倍。现在有了以下几个条件：1.每个数大于0 。2.两两不等。3.任意一个数不是其他数的两倍。每个数字可能是另两个之和或之差，第三个人能猜出144，必然根据前面三个条件排除了其中的一种可能。假设：是两个数之差，即x－y＝144。这时1（x，y>0）和2（x！＝y）都满足，所以要否定x＋y必然要使3不满足，即x＋y＝2y，解得x＝y，不成立（不然第一轮就可猜出），所以不是两数之差。因此是两数之和，即x＋y＝144。同理，这时1，2都满足，必然要使3不满足，即x－y＝2y，两方程联立，可得x＝108，y＝36。这两轮猜的顺序其实分别为这样：第一轮（一号，二号），第二轮（三号，一号，二号）。这样分大家在每轮结束时获得的信息是相同的（即前面的三个条件）。

那么就假设我们是C，来看看C是怎么做出来的：C看到的是A的36和B的108，因为条件，两个数的和是第三个，那么自己要么是72要么是144（猜到这个是因为72的话，108就是36和72的和，144的话就是108和36的和。）:

假设自己（C）是72的话，那么B在第二回合的时候就可以看出来，下面是如果C是

72，B的思路：这种情况下，B看到的就是A的36和C的72，那么他就可以猜自己，是36或者是108（猜到这个是因为36的话，36加36等于72，108的话就是36和108的和）：如果假设自己（B）头上是36，那么，C在第一回合的时候就可以看出来，下面是如果B是36，C的思路：这种情况下，C看到的就是A的36和B的36，那么他就可以猜自己，是72或者是0（这个不再解释了）：

如果假设自己（C）头上是0，那么，A在第一回合的时候就可以看出来，下面是如果C是0，A的思路：这种情况下，A看到的就是B的36和C的0，那么他就可以猜自己，是36或者是36（这个不再解释了），那他可以一口报出自己头上的36。（然后是逆推逆推逆推），现在A在第一回合没报出自己的36，C（在B的想象中）就可以知道自己头上不是0，如果其他和B的想法一样（指B头上是36），那么C在第一回合就可以报出自己的

72。现在C在第一回合没报出自己的36，B（在C的想象中）就可以知道自己头上不是

36，如果其他和C的想法一样（指C头上是72），那么B在第二回合就可以报出自己的

108。现在B在第二回合没报出自己的108，C就可以知道自己头上不是72，那么C头上的唯一可能就是144了。

伯乐选马

有25匹马，速度都不同，但每匹马的速度都是定值。现在只有5条赛道，无法计时，即每赛一场最多只能知道5匹马的相对快慢。问最少赛几场可以找出25匹马中速度最快的前3名？

答案：每匹马都至少要有一次参赛的机会，所以25匹马分成5组，一开始的这5场比赛是免不了的。接下来要找冠军也很容易，每一组的冠军在一起赛一场就行了（第6场）。最后就是要找第2和第3名。我们按照第6场比赛中得到的名次依次把它们在前5场比赛中所在的组命名为A、B、C、D、E。即：A组的冠军是第6场的第1名，B组的冠军是第6场的第2名……每一组的5匹马按照他们已经赛出的成绩从快到慢编号：

A组：1，2，3，4，5
B组：1，2，3，4，5
C组：1，2，3，4，5
D组：1，2，3，4，5
E组：1，2，3，4，5

从现在所得到的信息，我们可以知道哪些马已经被排除在3名以外。只要已经能确定有3匹或3匹以上的马比这匹马快，那么它就已经被淘汰了。可以看到，只有上表中粗体的那5匹马是有可能为2、3名的。即：A组的2、3名；B组的1、2名，C组的第1名。取这5匹马进行第7场比赛，第7场比赛的前两名就是25匹马中的2、3名。故一共最少要赛7场。

这道题有一些变体，比如64匹马找前4名。方法是一样的，在得出第1名以后寻找后3名的候选竞争者就可以了。

药片问题

某种药方要求非常严格，你每天需要同时服用A、B两种药片各一颗，不能多也不能少。这种药非常贵，你不希望有任何一点的浪费。一天，你打开装药片A的药瓶，倒出一粒药片放在手心；然后打开另一个药瓶，但不小心倒出了两粒药片。现在，你手心上有一颗药片A，两颗药片B，并且你无法区别哪个是A，哪个是B。你如何才能严格遵循药方服用药片，并且不能有任何的浪费？

答案：把手上的三片药各自切成两半，分成两堆摆放。再取出一粒药片A，也把它切成两半，然后在每一堆里加上半片的A。现在，每一堆药片恰好包含两个半片的A和两个半片的B。一天服用其中一堆即可。

汽车经过的概率

假设在一段高速公路上，30分钟之内见到汽车经过的概率是0.95。那么，在10分钟内见到汽车经过的概率是多少?(假设缺省概率固定)

答案：这题的关键在于0.95是见到一辆或多辆汽车的概率，而不是仅见到一辆汽车的概率。在30分钟内，见不到任何车辆的概率为0.05。因此在10分钟内见不到任何车辆的概率是这个值的立方根，而在10分钟内见到一辆车的概率则为1减去此立方根，也就是大约63%

位数问题

2^10000是几位数？

答案：2^10000 =10^(lg(2^10000)) =10^(10000*lg2) =10^(10000*0.30102999566) =10^(3010.2999566) 总共3011位

爱因斯坦谜语问题

今日题目：

这个问题出自爱因斯坦，据他说，98%的人都做不出来。
有一排五间房子，每一间房子的颜色都不同。在这些房子里住着五个不同国籍的人。每个人喂养了不同的动物，喜欢不同的饮料，抽不同的雪茄。

1. 英国人住在红色房子里。
2. 瑞典人养狗。
3. 丹麦人喝茶。
4. 绿色的房子在白色房子的左边。
5. 绿色房子的主人喜欢喝咖啡。
6. 抽“坡魔”牌雪茄的人养鸟。
7. 黄色房子的主人抽“顿山”牌雪茄。
8. 住在中间房子的人喝牛奶。
9. 挪威人住在第一间房子。
10. 抽“波兰斯”牌雪茄的人住在养猫的人旁边。
11. 养马的人住在抽“顿山”牌雪茄的人旁边。
12. 抽“蓝领”牌雪茄的人喝啤酒。
13. 德国人抽“王子”牌雪茄。
14. 挪威人住在蓝色房子旁边。
15. 抽“波兰斯”牌雪茄的人有一个喝水的邻居。

谁家养鱼？你是那2%的人吗？

答案：

人	颜色	雪茄	爱好	动物
挪威人	黄色	顿山牌	水	猫
丹麦人	蓝色	波兰斯牌	茶	马
英国人	红色	坡魔牌	牛奶	鸟
德国人	绿色	王子牌	咖啡	鱼
瑞典人	白色	蓝领牌	啤酒	狗

顺序题

下面是一个数谜。应该从左到右，从上到下。

       1
      1 1
      2 1
    1 2 1 1
  1 1 1 2 2 1
  ? ? ? ? ? ?
? ? ? ? ? ? ? ?

答案： 第一行是“两个一”（2 1）
第二行是“一个二，和一个一”（1 2 1 1）
因此第三行是“一个一，一个二和两个一”（1 1 1 2 2 1）
第一行是“三个一，两个二和一个一”（3 1 2 2 1 1）
第五行是“一个三，一个一，两个二和两个一”（1 3 1 1 2 2 2 1）

       1
      1 1
      2 1
    1 2 1 1
  1 1 1 2 2 1
  3 1 2 2 1 1
1 3 1 1 2 2 2 1

最大和问题

下面的方格阵需要在在数字库里选六个数字填上（三横三纵）。你可以每个数字用超过一次。当你填完了所有数字后，把他们的总和加起来，得到一个数和。这个数和最大可以是多少？

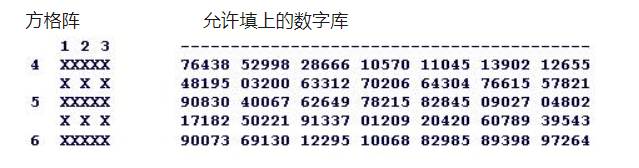
举例：用数字40067 04802 78215 每个两次

总和是73（当然可能有其它更大的总和的答案）

答案：这个是还没有查证的-我用了两个数字39543和89398。方格阵看起来就是这样：

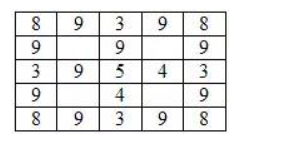
所以总数是147

旋转问题

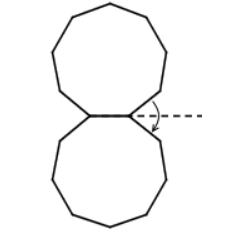
假设有两个一模一样的硬币 A 和硬币 B ，如果让硬币 B 不动，让硬币 A 贴着硬币 B 旋转一周，那么硬币 A 自身旋转了多少周？

答案：

一个常见的错误答案是“显然也是一周啊”，而实际上正确的答案是两周，如下图所示。我们有很多方法来解释这种现象，其中最传统的说法便是“公转了一周，自转了一周”。硬币 A 的运动是由两部分合成的，公转一周(想像一个人绕着地球走了一圈)，以及自转一周(想像一个轮子在地面上滚动了一周)。想像你是站在硬币 B 中心处的一个小人儿，看着硬币 A 贴着你脚下的硬币转动一圈。如果在此过程中，你始终面向硬币 A ，那么在你看来，硬币 A 似乎就是在长为 2πr 的平地上滚了一圈。而实际上，在观察硬币 A 的过程中，你自己也原地转了 360 度，因此从外面的人开来，硬币实际上转了两周。

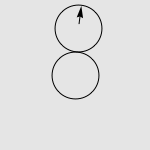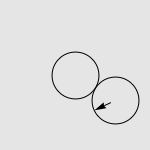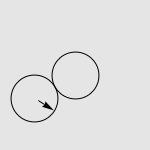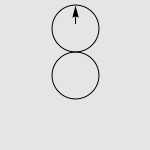
述问题的另一个简单而漂亮的解释方法，给出一幅图。

找规律

​ 101 103 107 115 122 127 137 148 （ ）

按照规律，括号里面应该填啥？

答案：

101,三个数字相加得2 （1+0+1）,所以,101+2=103
103,三个数字相加得4 （1+0+3）,所以,103+4=107
107,三个数字相加得8 （1+0+7）,所以,107+8=115
115,三个数字相加得7 （1+1+5）,所以,115+7=122
122,三个数字相加得5 （1+2+2）,所以,122+5=127
127,三个数字相加得10（1+2+7）,所以,127+10=137
137,三个数字相加得11（1+3+7）,所以,137+11=148

以此类推,于是得出括号里应该填入的数字是：161

概率问题

你有两个罐子，随机选出一个罐子，取出一个球，问给你50个红色弹球，50个蓝色弹球，如何放球可以使得取出红球的准确几率最大？

答案：一个罐子放一个红球,另一个罐子放49个红球和50个蓝球,概率接近75%.

这是所能达到的最大概率了。 原因：

放一个红球在一个罐子，两个罐子中取出红球的概率为50%*100%；另外一个罐子有49红+50蓝，两个罐子中取出红球的概率为：50% * （49/(49+50)）= 25%(约等于)，相加为75%。

实际上，只要一个罐子放<50个红球，不放篮球，
另一个罐子放剩下的球，拿出红球的概率就大于50%

分桃问题

有5只猴子在海边发现 一堆桃子,决定第二天来平分.第二天清晨,第一只猴子最早来到,它左分右分分不开,就朝海里扔了一只,恰好可以分成5份,它拿上自己的一份走了.第 2,3,4,5只猴子也遇到同样的问题,采用了同样的方法,都是扔掉一只后,恰好可以分成5份.问这堆桃子至少有多少只？

答案：这堆桃子至少有3121只。
第一只猴子扔掉1个，拿走624个，余2496个；
第二只猴子扔掉1个，拿走499个，余1996个；
第三只猴子扔掉1个，拿走399个，余1596个；
第四只猴子扔掉1个，拿走319个，余1276个；
第五只猴子扔掉1个，拿走255个，余4堆，每堆255个。
如果不考虑正负，-4为一解
考虑到要5个猴子分，假设分n次。
则题目的解: 5^n-4
本题为5^5-4=3121.

方法一：

设共a个桃，剩下b个桃，则b=(4/5)((4/5)((4/5)((4/5)((4/5)(a-1)-1)-1)-1)-1)，即

b=（1024a-8404）/3125 =>a=3b+8+53*(b+4)/1024，而53跟1024不可约，则令b=1020可有最小解，得a=3121

方法二：

设桃数x,得方程
4/5{4/5{4/5[4/5(x-1)-1]-1}-1} - 1=5n
展开得
256x=3125n+2101
故x=(3125n+2101)/256=12n+8+53*(n+1)/256
因为53与256不可约,所以判断n=255有一解.x为整数,等于3121

几何问题

第二个三角形图的问号方块是从哪里来的(各方块的分割是相同的)？

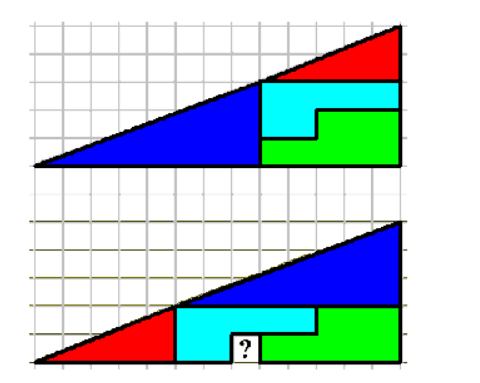
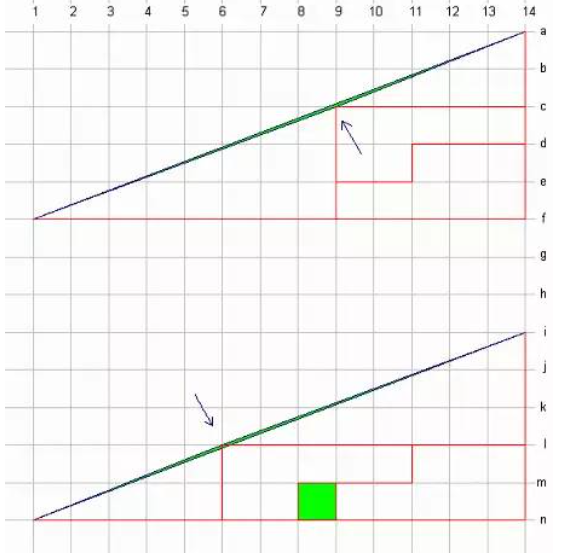
答案：它看起来像一个三角形，因为用了粗线条。直角三角形的斜边不是直线-是两条线组成的。箭头所指的就是。
这个64=65的几何谬论源自于四块图形的边，它们拼起来的长方形的对角线不是直线的，是一个菱形（钻石形），它的角度是:
arctan 2/3 - arctan 3/8 = arctan 1/46
这是小于1度15分。要非常精确的画图才能让我们区别这么小的角度。运用分析几何或者三角法，我们很容易可以证明“藏起来”的菱形就是那个棋盘上的小方格。

印花推理

超级高手拿了8个印花，4红4绿，把它们轻轻地粘在每一个逻辑推理者的前额上，每人两个。这样，他们每个人都可以看到别人前额的印花，但是看不到自己前额的两张和放在主持人口袋的两张。主持人顺序地问每个人知不知道他们头上的印花是什么颜色： A: 不知道 B: 不知道 C: 不知道 A: 不知道 B: 知道 那她的印花是什么颜色的呢?他是怎样知道的呢?

答案：B说：“假设我有红-红。A就会在第二轮说出来：”我看见B有红-红。。如果我也是红-红，那么四张红色都用了，那C就应该知道她的是绿-绿。但是C没有，所以我没有红-红。假设我有绿-绿。这样的话，C就知道如果她有红-红，我就可以看到四个红那么我就应该在第一轮就说出我有绿-绿 。相反，如果她有绿-绿（我们假定A可以看到C），那么B就已经看到四个绿，所以她就可以答出她有两个红。所以C知道，如果我有绿-绿和B有红-红，那如果我们两都在第一轮没有出声，那么她一定是绿-红。
B接着说：
“但是她（Ａ）并没有说她的是绿－红，所以我假设我有红－红肯定是错的。那么同样的推理用在假设她有绿－绿，那么我的肯定是绿－红。”
所以Ｂ有绿－红，但是我们不能肯定知道其他人的分配如何。

光环颜色

圣诞树上有四个天使（除了其他的东西）。两个有蓝色的光环，两个有黄色的光环，但是没有一个能看到他自己背后光环的颜色。天使A在树的最高处，他可以看到挂在下面的天使B和C。在下面挂着天使B，他只能看见在他下面的天使C。天使C看不到任何天使，因为天使D挂在一个横枝上（没人可以看到他，他也看不到其他人）。

哪一个天使将首先说出他自己光环的颜色呢？

答案：有两个可能的答案：
１　如果天使Ｂ和天使Ｃ有同样颜色的光环，那么天使Ａ肯定马上说出他自己的颜色（不同于其他的颜色），
２　如果天使Ｂ和天使Ｃ有不同颜色的光环，那么天使Ａ就不肯定和沉默，那么这是给天使Ｂ的一个信号，那么Ｂ（能看到天使Ｃ）就知道他自己的颜色（不同于天使Ｃ）。

几何问题

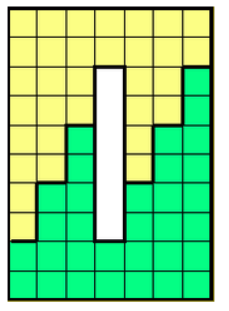
将这个中间有个洞的长方形分成两半，使得到一个8x8的中间没洞的正方形。

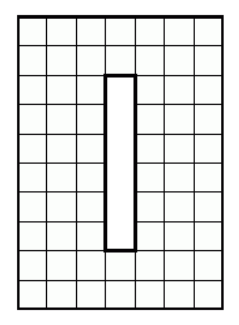
答案：

字母交换问题

在每一横列和每一纵列填上A,B,C,D,E一次(在第一个方格里只填A,B,C,D)。在方阵外面的字母是提示从那个方向起首的字母，比如说，在第三个方阵中，D必须是第一行第三行最左边的字母，C必须是第一和第二列的最后一个字母。

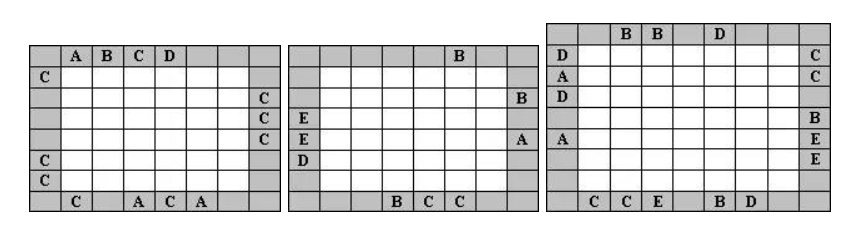
答案：

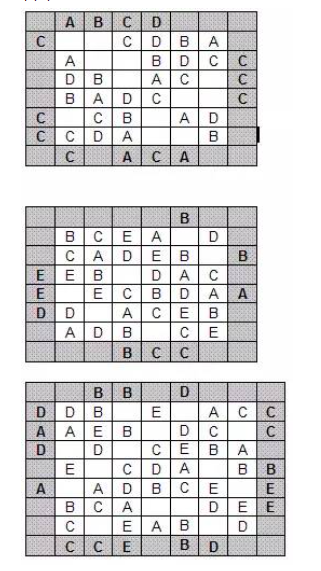
智力问题

有一个老实人（总是说真话），一个说谎者（总是撒谎），和一个有时说真话，有时说假话的人。你可以问三条答案是“是”还是“不是”的问题来分辨谁是谁。每一次你只能问一个人一条问题（你自己选）。你可以问同样一个问题多过一次，但是这是算在你问话的总和上的。
你会问什么和问谁？

答案：

这里有6种排列的情况（T代表老实人，R代表随机回答的人，L代表说谎者）：TRL, TLR, LTR, LRT, RTL, RLT
有8种可能组合的答案
理论上，你是可以找出8种组合答案对应的排列情况，但是，因为随机回答的人的答案不可靠，我觉得这是不可能的。在任何一个答案里，随机回答的人总是可能说正确或者错误的话。你不可能知道他什么时候说真话，什么时候说假话。所以，你不可以分出哪组答案对应哪个排列，所以永远都不知道谁是谁。
一分钟后，我就看出了我自己推理上的问题。我总是去想不管排列的情况怎样，老实人和说谎者说出的答案是一样的时候。我看到了如果你可以让老实人和说谎者给出一个是/不是的答案，那么你就可以找出随机回答人的无用的答案了。唯一一个办法是问他们自己排列的情况。
所以：
问1：说谎者是不是站在随机者的右手边（如果他们对着我们的话，就是左手边）。
那么答案就可以告诉你排列的情况分类：
如果答案“是”，那么就是老实人说的真话，说谎者说的假话，或者随机回答的人没有意义的答案，所以：TLR, LTR 或者 RTL, RLT。
如果答案“不是”，那么就是老实人说的真话，说谎者说的假话，或者随机回答的人没有意义的答案，所以：TRL, LRT 或者 RTL, RLT。
现在我们知道，通过1可以避免随即回答的人无意义的答案。我们现在可以问老实人或者说谎者“老实人是不是排头？”如果答案“是”，我们问第二个人，如果答案“不是”，我们问第三个人。
现在的答案可以告诉我们更多的信息。如果答案“是”，那么就是老实人在说真话，如果答案是“不是”，就是说谎者在说谎。所以基于我们问的是谁，我们现在知道：
是，是：只能是LTR，或者是RTL
是，不是：TLR, RLT
不是，是：LRT, RLT
不是，不是：TRL, RTL
现在任何可以分开这两种可能的问题都可以问了-只是要注意避免随机回答的人无意义的答案。
举个例子：
是，是，- 如果#1是说谎者，问#2。（我们知道#2是老实人，是说真话的）-是=LTR，不是=TLR。
不是，是，- 如果#1是老实人，问#2.（我们知道#2是说谎者，说的是谎话）-是=LRT,不是=RLT。
不是，是，- 如果#1是说谎者，问#3.（我们知道#3是老实人，是说真话的）-是=LRT,不是=RLT.
所以我们就知道排列的顺序和谁是谁了。

分类问题

三个盒子的标签都贴错了，你必须把它们弄正确。标签上这样写：

为了得到你需要的信息，你可以从一个盒子里移除一件物品。你不可以看进盒子里，也不可以拿起来或者摇晃它。你可以做到吗？如果可以，怎样做？如果不可以，为什么？

答案：从3号盒子里拿一样东西出来。
这样东西告诉你应该在3号盒子上贴什么标签。
把钉子和螺丝的标签移到另外的那个盒子，再把那个盒子的标签移到剩下的那个盒子上。
举例：你从3号盒子里拿出了钉子。
那么把1号盒子的钉子标签移到3号。
你不可以把钉子和螺丝的标签移到1号：这样只是1号和3号的互换，但是三个盒子都必须要纠正的。
所以把它移到2号盒子，然后螺丝的标签移到1号盒子。
[1号盒子] 螺丝
[2号盒子] 钉子和螺丝
[3号盒子] 钉子

男女比例

有一个人们只想生男孩子的国家，他们在有儿子之前都会继续生育。如果第一胎是女儿，他们就会继续生育直到有一个儿子。这个国家的男女儿童比例是多少？

答案：

1、 假设一共用10对夫妻，每对夫妻有一个孩子，男女比例相等。(共有10个孩子，5男5女)；

2、生女孩的5对夫妻又生了5个孩子，男女比例相等。(共有15个孩子，男女儿童都是7.5个)；

3、生女孩的2.5对夫妻又生了2.5个孩子，男女比例相等。(共有17.5个孩子，男女儿童都是8.75个)；

4、因此，男女比例是1:1。

填数字

找规律填数 5 10 26 65 145 （）？

答案：答案 5 10 26 65 145 （290）

2^2+1；3^2+1； 5^2+1； 8^2+1； 12^2+1 ；17^2+1

多米诺骨牌

这图片上有28对多米诺骨牌(0-0, 0-1, 0-2, …, 6-6).可惜不能在图里标出来。你自己看看能不能找出28多米诺骨牌在哪里。
把它们标出来？

答案：

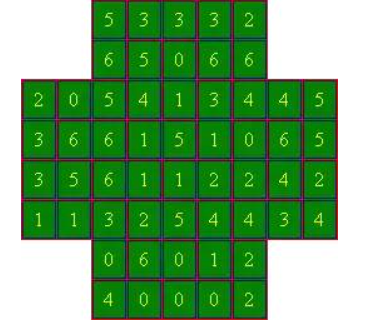
六角形问题

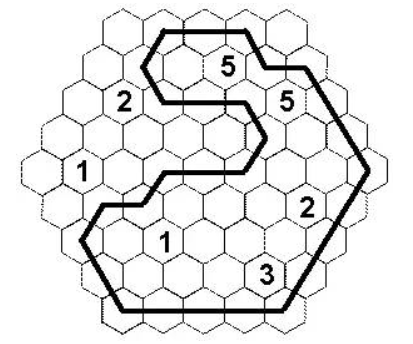
找一条环线路径是符合以下限制的。路径通过六角形的中心从一个六角形到相邻的六角形，不重复经过任何一个六角形，也不经过有数字的六角形，也不突然拐弯（比如拐60度的角度）。每个数字标志着相邻的有多少个六角形是路径的一部分。

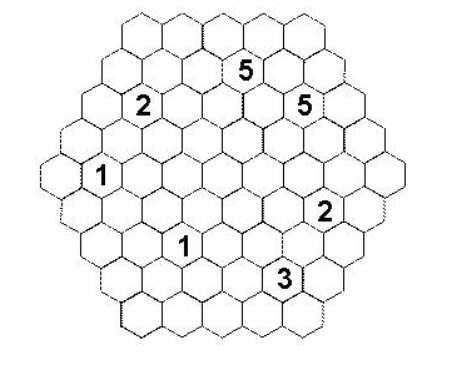
答案：

抉择问题

你在一个游戏节目上，有三道门。主持人告诉你在一个门的后面是一部车，其它两个门后面是两支山羊。如果你选了车你就赢了。当你选了一扇门后，主持人开了另一道门，是一只山羊。然后她说他给你机会选哪道门. 你应该怎样做？
提示：不是你想的二分一的答案。

答案：你应该改开另外一扇门。跟直觉相反，改开另一扇门事实上可以让你赢的机会加倍。
这个问题就是蒙提霍尔问题。理解的关键在于主持人知道车和羊的位置。这一点影响到他的行为还有公平性。
以下是所有你会遇到的情况和解释你为什么要改开另一扇门。

• #2门有羊B（概率是1：3）- 主持人开了#1门有羊A（1：1） - 车在#3门后（1：1）-改开另外一扇门就赢了车-全部机会(1:3 x 1:1 x 1:1 = 1:3)
• #2门有车（概率是1：3）- 主持人开了#1门有羊A（1：1） - 羊B在#3门后（1：1）-不要改开另外一扇门就赢了车-全部机会(1:3 x 1:2 x 1:1 = 1:6)
• #2门有车（概率是1：3）- 主持人开了#1门有羊B（1：2） - 羊A在#3门后（1：1）-不要改开另外一扇门就赢了车-全部机会(1:3 x 1:2 x 1:1 = 1:6)
  所以如果你改开另一扇门有(1:3 + 1:3 = 2:3)的机会赢了车，如果你坚持不改，只有(1:6 + 1:6 = 1:3)的机会会赢。

数据处理

给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，让你找出a、b文件共同的url？

答案：

方案1：可以估计每个文件安的大小为5G×64=320G，远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。

遍历文件a，对每个url求取hash(url)%1000，然后根据所取得的值将url分别存储到1000个小文件（记为a0,a1,…,a999）中。这样每个小文件的大约为300M。

遍历文件b，采取和a相同的方式将url分别存储到1000小文件（记为b0,b1,…,b999）。这样处理后，所有可能相同的url都在对应的小文件（a0vsb0,a1vsb1,…,a999vsb999）中，不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。

求每对小文件中相同的url时，可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url，看其是否在刚才构建的hash_set中，如果是，那么就是共同的url，存到文件里面就可以了。

方案2：如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的url（注意会有一定的错误率）。

头巾问题

有三个白人被一个印第安反对部落俘虏了。部落的首领愿意把他们放了，所以他把他们领到一个没有亮光的帐篷里。他给了每人一条头巾（他有三条头巾，三白二红-所以有两条是没用到的）。然后他们排着队出去，这样，每个人都可以看到前面人的头巾颜色，但是看不到自已头巾的颜色（第一个走出去的人看不到任何头巾，第二个人可以看到第一个人的头巾，第三个人可以看到前面两个人的头巾）。如果有其中一个人说出了自己头巾的颜色，那所有人的可以被放了。几分钟的沉默后，其中一个人说：“我头巾的颜色是。。。”。
他头巾是什么颜色？你是怎样推敲到的？

附加条件：
你可以设想所有的囚犯都是聪明的，而且他们对同伴的智慧也很有信心。
他们猜错了一次就会被监禁。
所有人加起来只能猜一次。
所有人都想被释放。

答案：

第一个人（他看不到任何的头巾）是这样想的：
最后一个人不出声，说明了他不知道，因此他看到的最少有一条头巾是白色的。中间的人也不出声（他也知道最后一个人看到的是什么）。如果我的头巾是红色的，那么中间的那个人就知道他的是白的。然而，没有人说话，那么我的头巾一定不是红的－我的头巾是白色的。

磁铁问题

这是一个在美国科学杂志上发表的逻辑推理题。
你在一个除了两根铁针就没有其它金属的房间里。只有一根铁针是磁铁。
你怎样鉴定呢？

答案：你可以把铁棒用一根绳子吊起来看看哪一根指向北面（或者只挂一根铁棒）。
嘉德讷给出另外一个方法：拿起一根铁棒用它的一头去触碰另一根铁棒的中间。如果它们互相吸引，那么拿在你手上的就是磁铁。
一块真的磁铁的磁场会在它的两级，而不在它的中间。所以就像刚才所说的，如果你拿着的是一根铁条，去触碰磁铁的中心，那么铁条是不会被吸引的。这就是假定磁铁的两级在它的两头。如果它的两级在整条磁铁上，那么这种方法就比较难了。
如果是这样，那你可以抓住一根铁棒，用它的一头去靠近另一根绕着它的轴线旋转着的铁棒的中心。如果旋转着的铁棒是磁铁，那么磁力会随着它的旋转而变化。如果旋转着的那根不是磁铁，那么磁力的大小会保持不变（前提是你可以保持它们的位置不要移动）。

最大的100个数

用快速有效的方法从100w个数中找出最大的100个数？其复杂度为多少?

答案：

方案1：用一个含100个元素的最小堆完成。复杂度为O(100w*lg100)。

​ 方案2：采用快速排序的思想，每次分割之后只考虑比轴大的一部分，知道比轴大的一部分在比100多的时候，采用传统排序算法排序，取前100个。复杂度为O(100w*100)。

​ 方案3：采用局部淘汰法。选取前100个元素，并排序，记为序列L。然后一次扫描剩余的元素x，与排好序的100个元素中最小的元素比，如果比这个最小的要大，那么把这个最小的元素删除，并把x利用插入排序的思想，插入到序列L中。依次循环，知道扫描了所有的元素。复杂度为O(100w*100)。

判断2的幂

给出一行C语言表达式，判断给定的整数是否是一个2的幂？（一行是指一句代码）。

答案： (b & (b-1)) == 0 ，解析：由于2的幂都是10 ，100， 1000， -1与原数相&后必定为0。

逻辑推理

三个逻辑推理高手想找出谁最厉害。于是他们请了超极高手来做裁判一比高下。超极高手把他们带到一个黑房间，说：“我会在每个人的额头上画一个红点或者蓝点。当你们走出这间房子的时候，你们可以看到一个红点以上的，举起手。哪一个最先说出自己头上的点是什么颜色的就赢了。然后他在每个人头上都只点了红点。当他们走出房间的时候，他们都举起了他们的手，过了一会儿，一人说：“我的头上是红点。”
他是怎样知道的？

答案：假定C是我自己，那么A，B，和我自己都看见了大家的手都举起来了，这说明了每个人都看到了至少一个红点在别人的额头上。如果我（C）头上是蓝点，那么A和B都看到三个人的手举起来，一个红点（他们举起手的原因）和一个蓝点（在我额头上）。那么A和B都会这样想：大家都举了手，而我看见了一个红点和一个蓝点，那额头是红点的人也举了手，证明他在某处看到了红点，那就只能是在我的额头上。
但是A和B都没有说话，这就说明他们都不是很肯定。那如果我的额头上是蓝点，他们就会肯定了。所以我额上的是红点。