常见算法题。
鸡兔同笼
故事起源
有若干只鸡和兔在一个笼子里,从上面数有35个头,从下面数有94只脚。问笼中各有多少只鸡和兔?
分析
先假设有x只兔子,y只鸡。
则根据头的数量可得到一个信息:x+y=35。
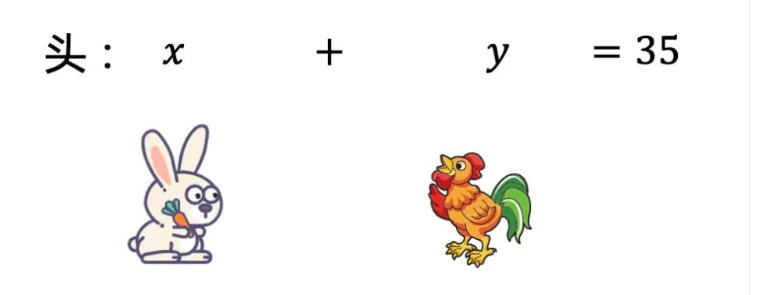
再根据脚的数量可得到一个信息:4x+2y=94。
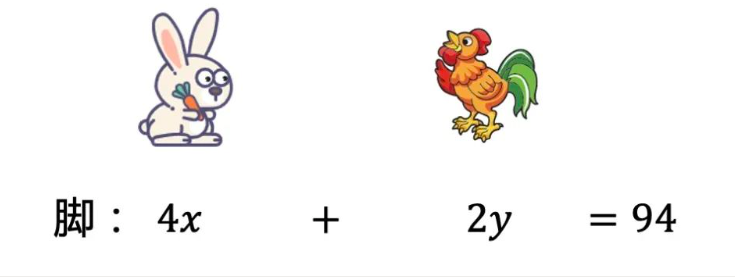
于是我们把这个问题就变成了一个初中数学问题,即二元一次方程求解。
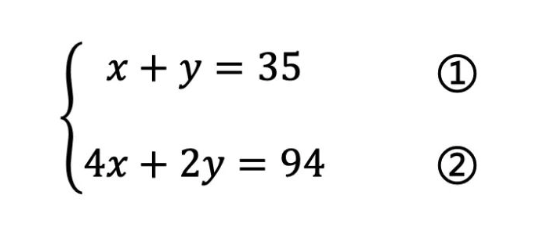
求解过程也比较简单,通过变形即可。
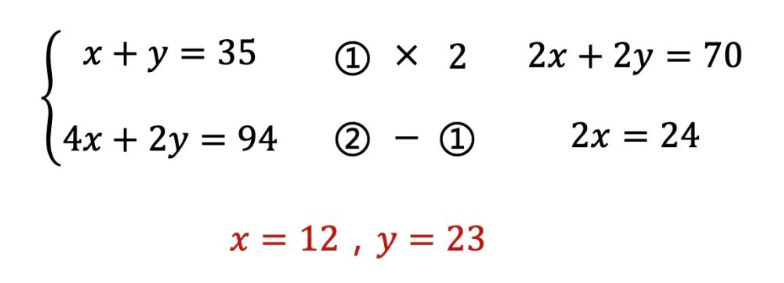
生活中有很多的问题都可以演变成一个方程求解,比如一般的情况如下。
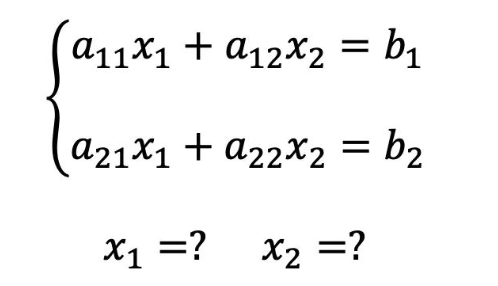
那有没有快速求解的方法呢?作为一个大学生,肯定要用一些更高级的方法啦
方程求解
从上面可以得出通过消元减少未知数,为消去x2,以a22与a12分别乘上两式,然后相减得到下式。
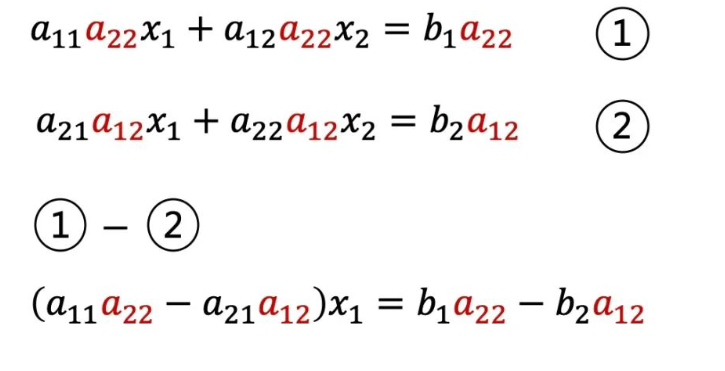
同理为消去x1,可得到下式。
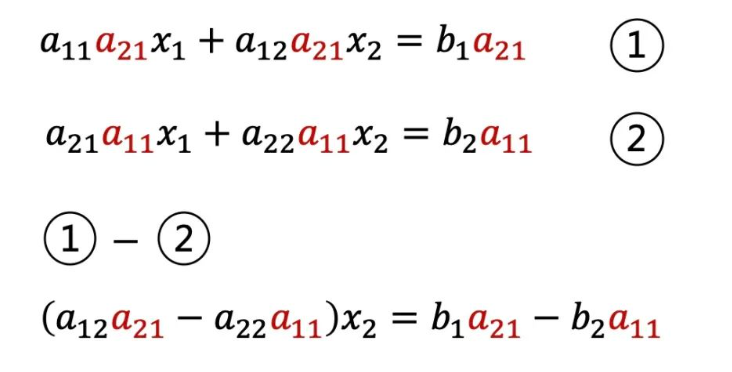
然后就得到了一般解。
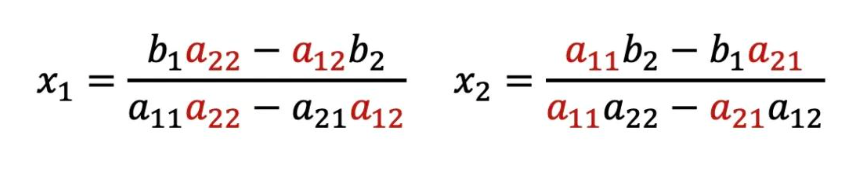
不难发现x1和x2的分母都是一样的,而且只有左边的系数,那能否把这个规律更加通俗易懂的总结一下呢?这就要说到大学中一个非常重要的知识,行列式。
行列式
先把系数和未知数分离开。

对一个2行2列的矩阵定义这样一种运算规则,交叉相乘再相减,这就叫作二阶行列式。
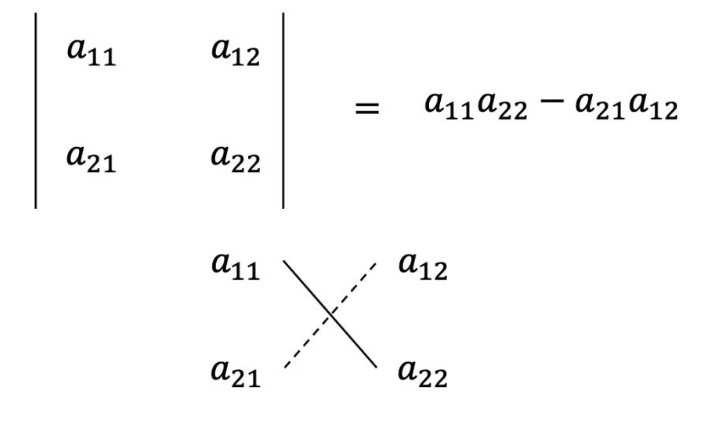
实线为主对角线,虚线为副对角线,即主对角线之积减去副对角线之积。
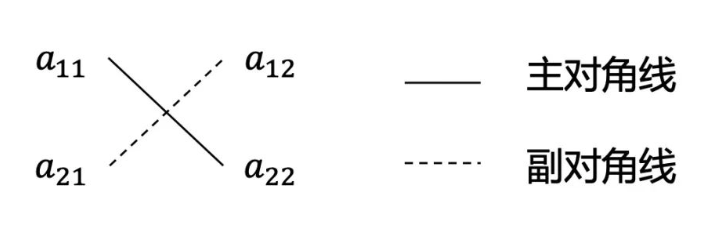
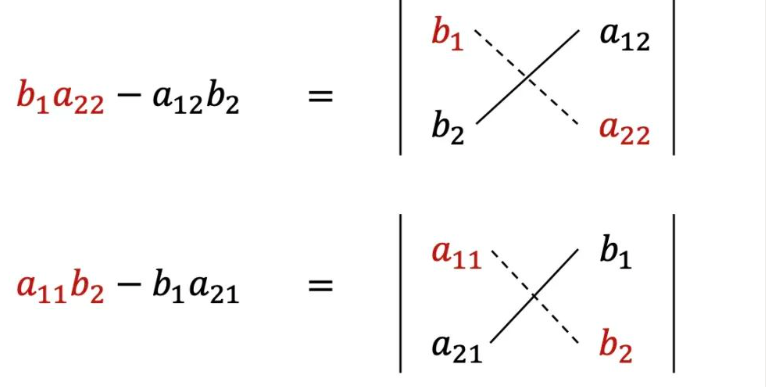
同样x1和x2的分子也可以用二阶行列式表示。x1的分子是用b1,b2替换第1列,x2的分子就是用b1,b2替换第2列。
则x1和x2就可以用二阶行列式表示出来。
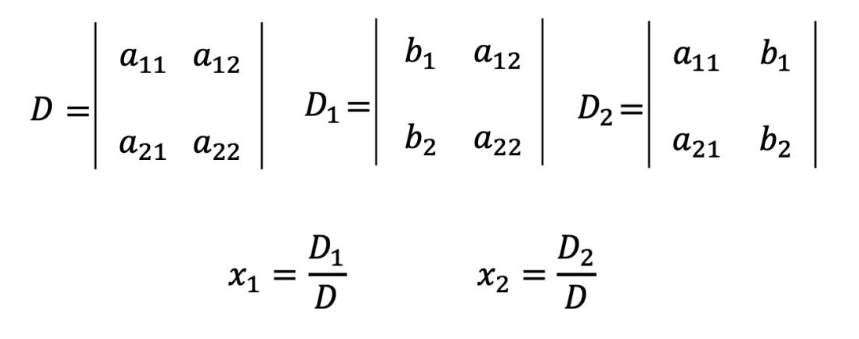
现在我们已经学会了用二阶行列式解二元一次方程
应用
现在我们用行列式来解文章开头的方程,先计算对应的3个行列式。

再通过上面的值求出未知数。
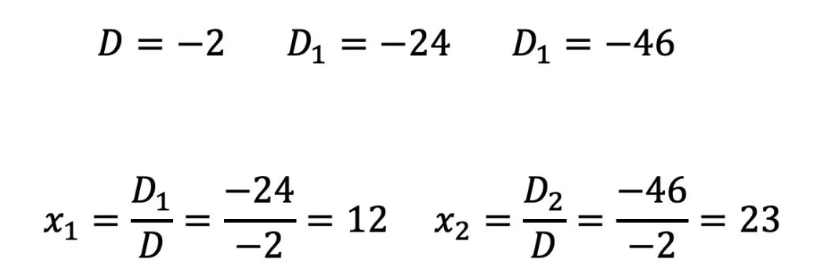
是不是感觉方便多了,知识就是力量,高等数学果然不一样。小学生都可以学会的技能,可以广泛的应用到生活中。
我猜肯定有同学会问,如果有3个未知数甚至更多怎么办呢,有没有3阶行列式,n阶行列式呢?答案肯定是有的啊,非大学与大学数学知识最大的一个区别就是推广,大学以下只教你1,2,3,大学以上教你m,n。
总结
数学知识真的非常重要,但在学校那会单纯的学习1+1=2真的枯燥和乏味,如果结合生活中的应用场景,就会变得很有意思了。
140 克盐如何 3 次分成 50 克、90 克?
故事起源
有一个天平,7克、2克砝码各一个,如何只用这些物品三次将140克盐分成50g,90g各一份?
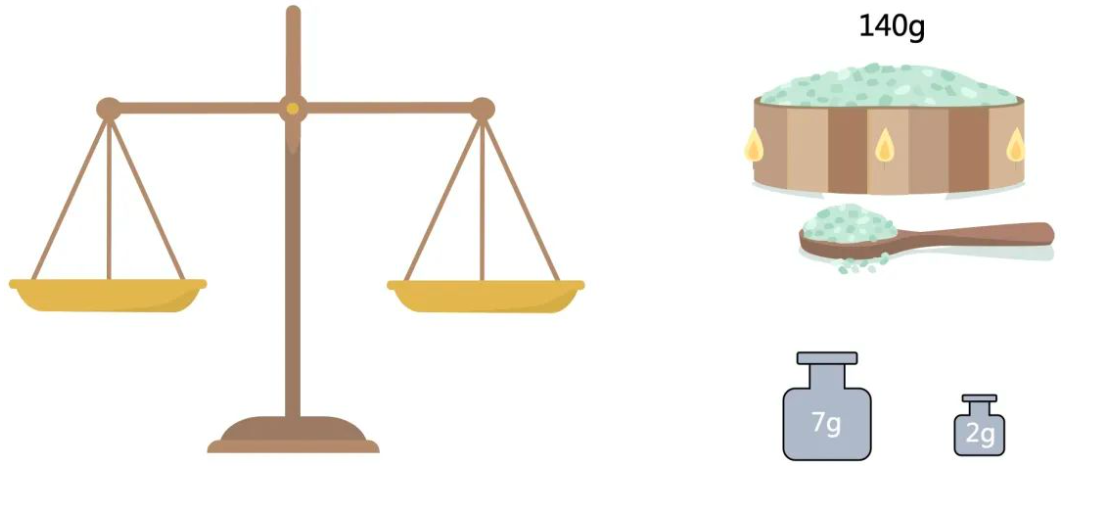
不用砝码的情况
天平是用于衡量是否相等,所以如果不借助砝码,只能等分。
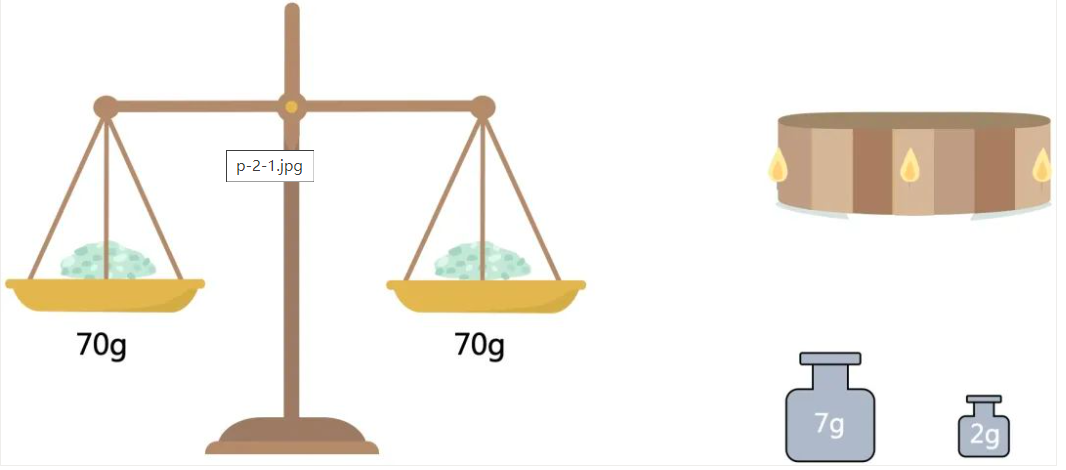
如第一次分成70和70,第二次可以分成35和35,第三次可以等分35或者105。

但上面分出的数值,是无法组合成50或者90的。所以接下来就考虑借助砝码的情况。
借助砝码的情况
方法一
砝码和盐各放一边,可以得到2,7,9,x-2,x-7,x-9克重量。
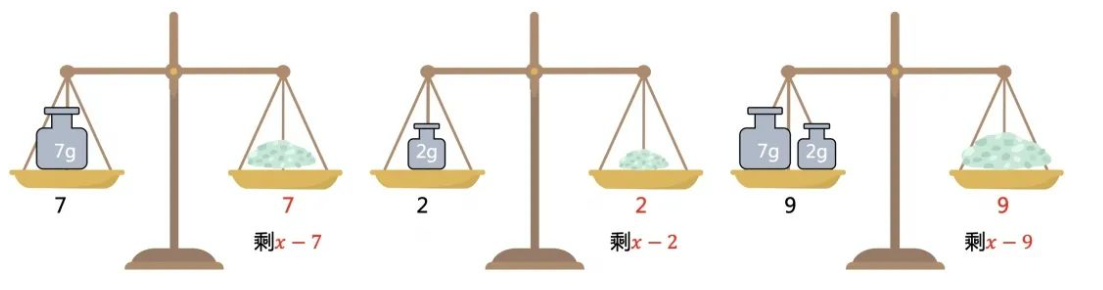
方法二
砝码放一边,将克盐放两边,可以得到如下重量。
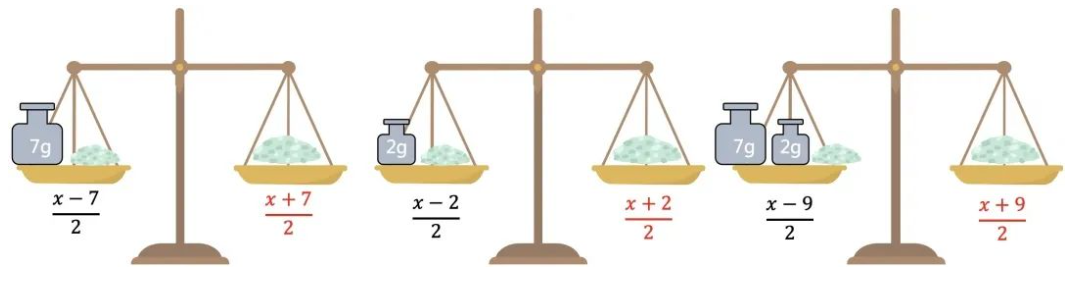
方法三
砝码放两边,盐放一边或者两边.
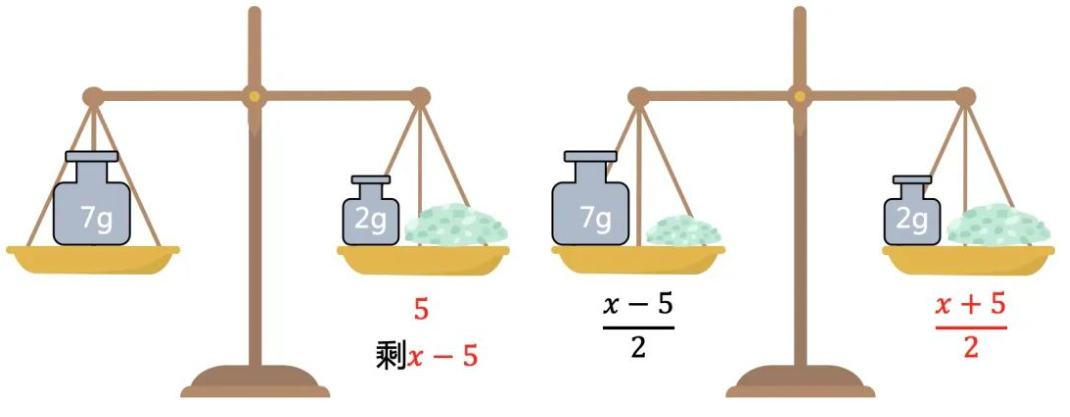
这样就把所有的可能枚举完了,接下来就要看如果用这些方式组合成目标数。
用码组合
35克
前2步不用砝码可以得到35克,再结合砝码可以得到如下。

可以看到红色产生了15克,加上35克刚好50,这就有一个解。
70克
前1步不用砝码,能得到70克,再结合砝码。
称一次:
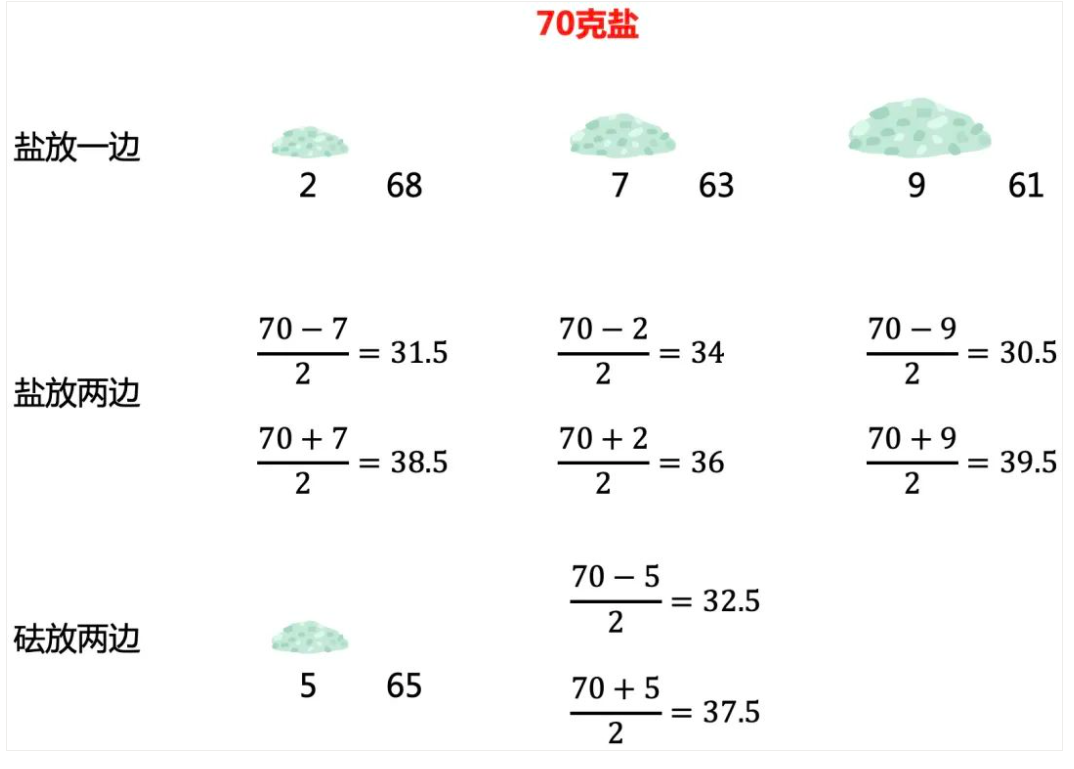
称二次:
根据上面一次的结果来看,盐放两边和砝放两边都无法再组合。但如果盐放一边可以多一个砝。
刚好发现如果先分成9+61。再用多的9+2来分61刚好得50,又得一个解。
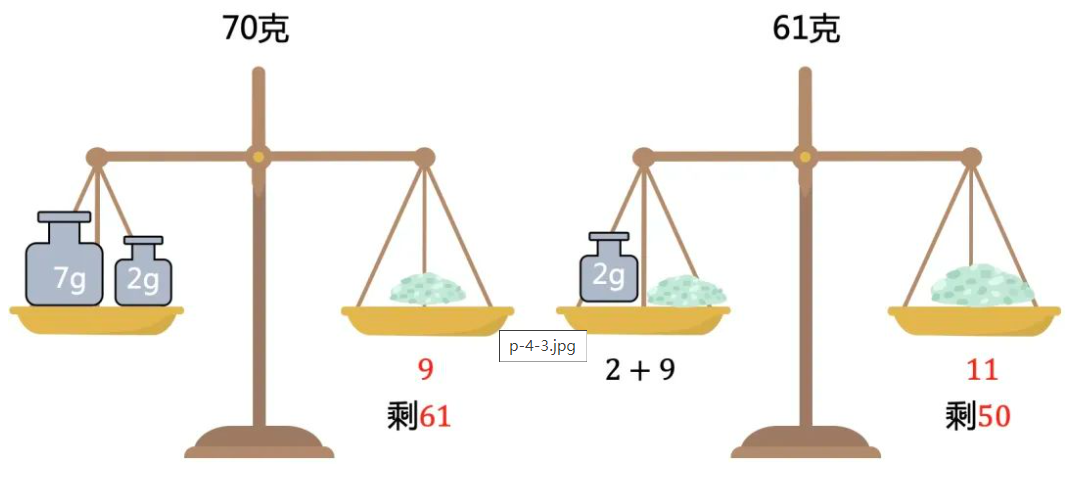
140克
一开始就借助砝码得到不同的重量,不过这个解很难直接看出来。

用砝码拼凑
如果按下面的方法称一次,就会得到相同重量的盐,所以也可以把右边的盐当成一个砝码,这样称三次就不只是2个砝码了。
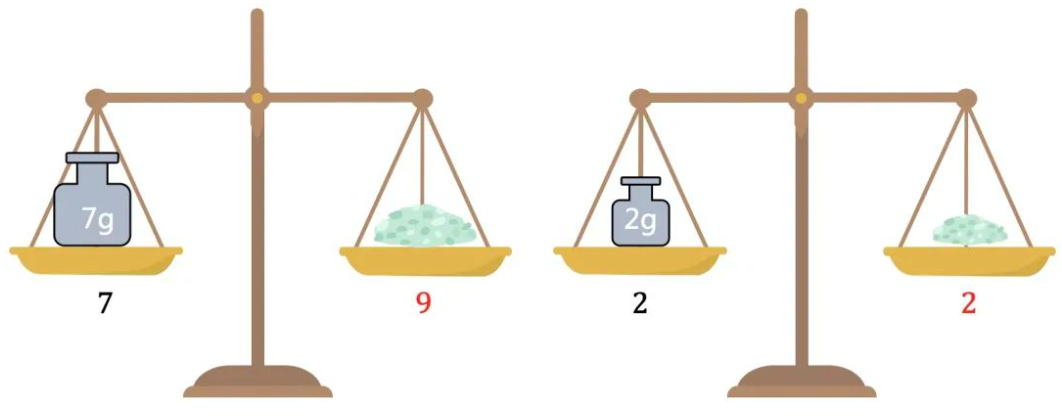
接下来我们用这种方法,看能称出哪些重量的盐。
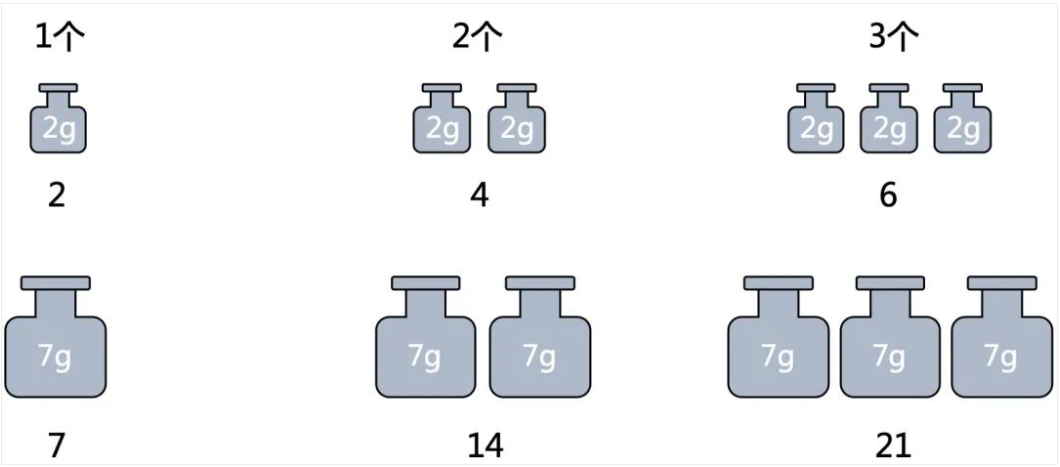
然后我们就要用这些数字,看能否组合成50或者90。
很容易可以发现下面的红色加起来刚好就是50。
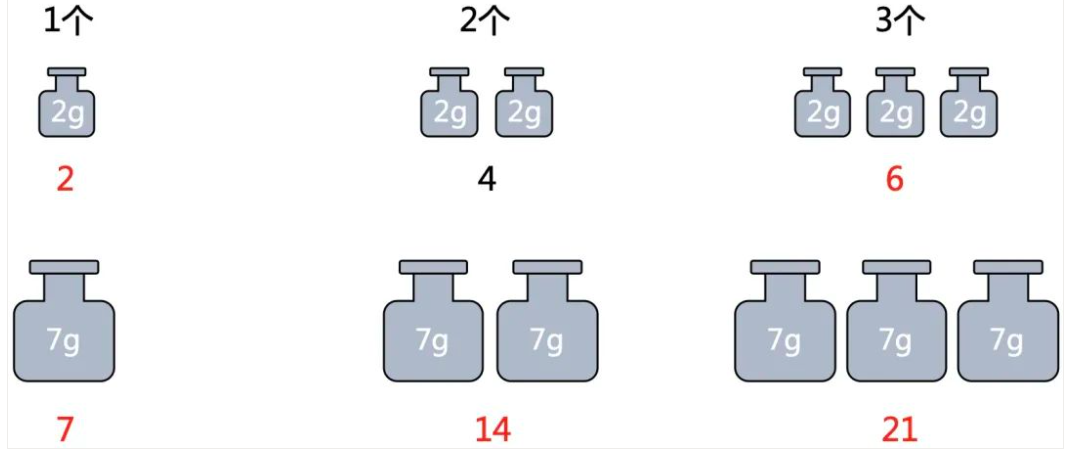
也就是要4个2g的,和6个7g的。
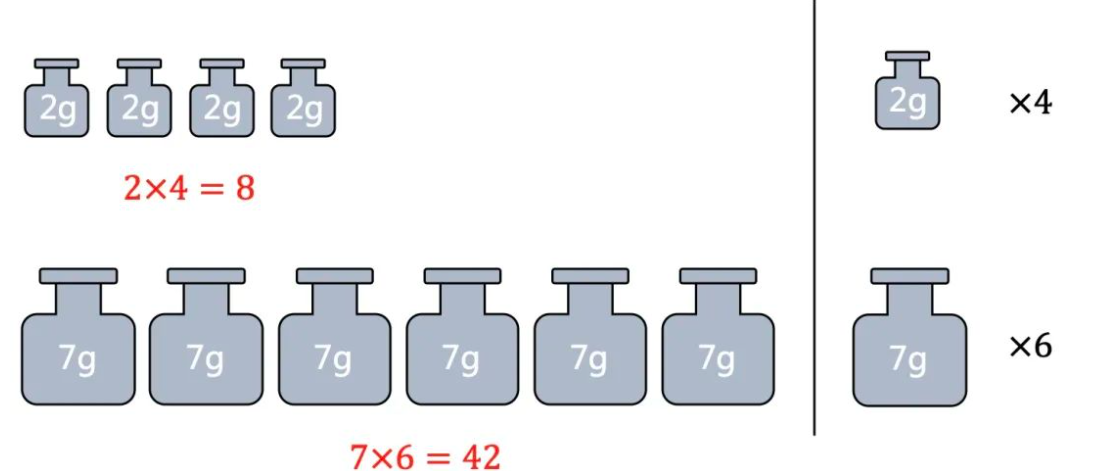
如果用数学方法也可以得到上面的结论。
只有2个砝码,2克和7克的,如果用这2个来随意组合。
设x个2克,y个7克,即2x+7y=50,整数解如下:
| x | y |
|---|---|
| 18 | 2 |
| 11 | 4 |
| 4 | 6 |
因为只能称三次,前两组解是无法组合出这么多的,所以得到2x4+7x6=50。
组合一
天平称一次,可以将重量翻一倍。上面砝码是分开的,次数不够,所以需要合并。
重新组合成(2x2+7x3)x2。
那么最后一次要先得到2x2+7x3=(2+7)+(2+7)+7,又得到一组解。
具体过程如下:
第一次,第二次:
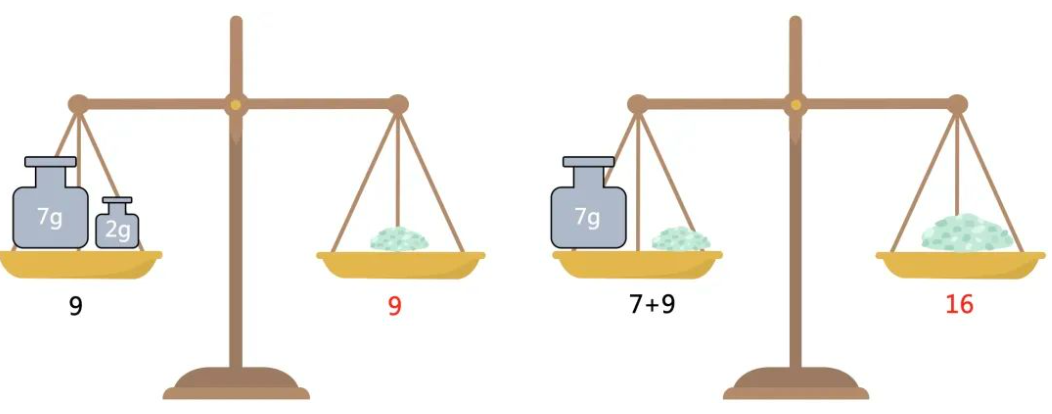
第三次:

组合二
这组解也很难直接发现,因为要利用到砝码的5g差。
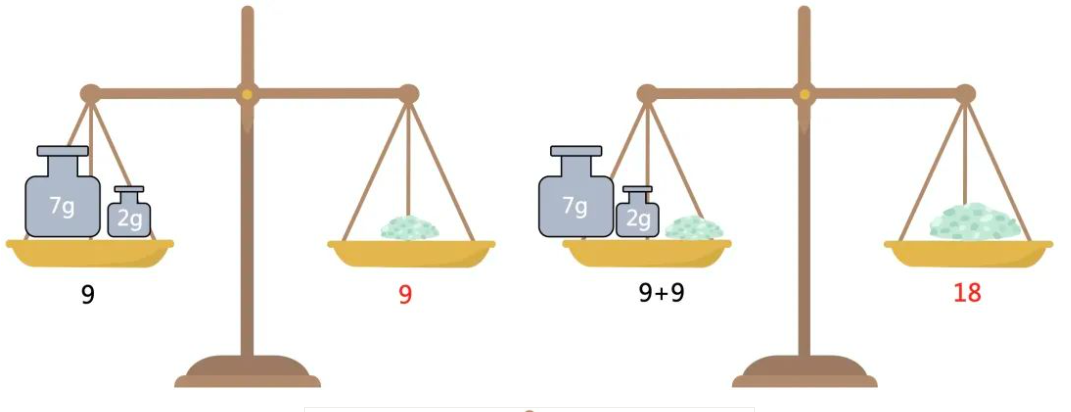

过程抽象
整个过程其实就是一个搜索的思路,DFS或者BFS,但我想用动态规划里面的语言来抽象描述一下。
初始条件:开局一个天平,2,7克砝码,140g盐。
决策:第2,3小节里,不用砝码,和借助砝码的多种方法。
阶段:总共称三次,每一次就是一个阶段。
状态:每过一个阶段,能得到的不同的情况。
状态转移:根据上面不同的决策转移到下一个状态。
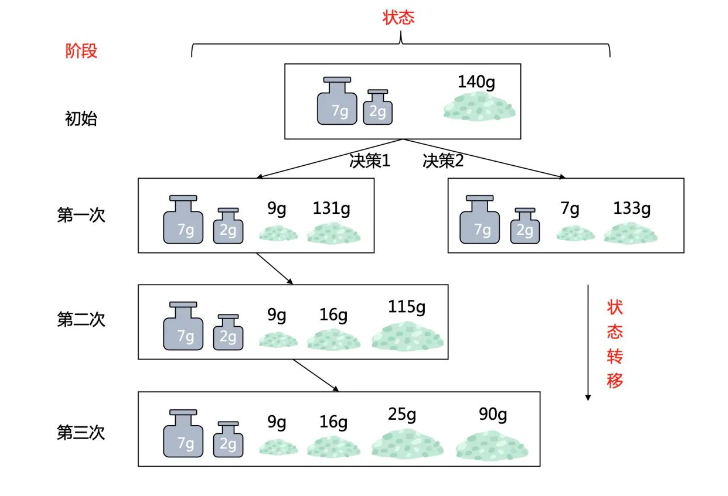
总结
初始条件很简单,但决策很多,每过一个阶段,状态也会成倍的增加。而且阶段有3层,最后的状态数已经很多了,人工模拟还是比较难的。最好的方法还是参考4、5小节,看能否快速找到一个可行解。

