leetcode算法练习。
1135最低成本联通所有城市
最小生成树 图的生成树是一棵含有其所有的顶点的无环联通子图,一幅加权图的最小生成树( MST ) 是它的一颗权值(树中所有边的权值之和)最小的生成树。
并查集 并查集是一种树型的数据结构,用于处理一些不相交集合的合并及查询问题。常常在使用中以森林来表示。
方法一:Kruskal 算法
思路
根据题意,我们可以把 n 座城市看成 n 个顶点,连接两个城市的成本 cost 就是对应的权重,需要返回连接所有城市的最小成本。很显然,这是一个标准的最小生成树,首先我们介绍第一种经典算法: Kruskal 算法。
既然我们需要求最小成本,那么可以肯定的是这个图没有环(如果有环的话无论如何都可以删掉一条边使得成本更小)。该算法就是基于这个特性: 按照边的权重顺序(从小到大)处理所有的边,将边加入到最小生成树中,加入的边不会与已经加入的边构成环,直到树中含有 n - 1 条边为止。这些边会由一片森林变成一个树,这个树就是图的最小生成树

算法
- 将所有的边按照权重从小到大排序。
- 取一条权重最小的边。
- 使用并查集(union-find)数据结构来判断加入这条边后是否会形成环。若不会构成环,则将这条边加入最小生成树中。
- 检查所有的结点是否已经全部联通,这一点可以通过目前已经加入的边的数量来判断。若全部联通,则结束算法;否则返回步骤 2.
1 | class Solution { |
复杂度分析
时间复杂度:O(eloge+e∗n),其中 e 为边的数量,n 为城市的数量。排序的时间复杂度为 O(eloge),我们需要遍历 e条边。对于每条边,查找两个端点的根结点最多需要经过 2n个结点。所以时间复杂度最坏为 O(e∗n)。
空间复杂度:O(n),需要大小为 n 的并查集结构存储点的关系,其中 n 为城市的个数。
方法二:Kruskal 算法 + 加权 Union 算法
思路
方法一我们检查环的过程中,最坏的情况下每次需要遍历所有的边,形成一个永远只有左子节点的树。为了避免形成这样的结构,我们可以记录每一颗树的大小并且总是将较小的树连接到较大的树上,这个算法就叫加权 Union 算法。该算法需要添加一个数组记录树中的节点数,并且在联通的时候比较节点个数,将较小的树连接到较大的树上。
1 | public int minimumCost(int n, int[][] connections) { |
复杂度分析**
时间复杂度:O(e(loge+logn)),使用加权 Union 算法后,find 操作的时间复杂度为 O(logn)。另外此时的时间复杂度还受排序操作制约,排序操作复杂度为 O(eloge),综合起来时间复杂度为 O(e(loge+logn))
空间复杂度:O(n),需要大小为 n 的并查集结构存储点的关系,其中 n 为城市的个数。
方法三:Kruskal 算法 + 加权 Union 算法 + 路径压缩
思路
考虑在方法一和方法二中我们使用的 find 函数,可以发现,一些路径是被重复寻找了的。
举个例子,假设在并查集中有四个结点,其中 1 的父亲是 2,2 的父亲是 3,3 的父亲是 4。那么我们在以后每次寻找 1 所在的集合时,都需要经过 1-2-3 这条路径;查找 2 所在的集合时,都需要经过 2-3-4 这条路径。可以想到,在一个大型图中,查找根结点的路径中会存在大量与此类似的重复查询。
而事实上,我们通过一个简单的操作来避免这样的重复查询:我们可以在 find 函数结束的时候,将路径上所有的结点,修改为根结点的直接子结点。这样,我们下次查询时,就可以直接找到刚才找到的根结点,不需要再查询一次相同的路径了。
1 | public int minimumCost(int n, int[][] connections) { |
复杂度分析
时间复杂度:O(e∗(loge+α(n))),其中 e 为边的数量,n为城市的数量。经过优化后,find 操作的时间复杂度为 O(α(n)) ,其中 α为反阿克曼函数,其增长极其缓慢,也就是说其单次操作的平均运行时间可以认为是一个很小的常数。具体的证明过于复杂,了解结论即可。此时算法的总体时间复杂度仍然受排序操作制约,为 O(eloge),综合可得时间复杂度为 O(e∗(loge+α(n)))。
空间复杂度:O(n),需要大小为 n 的并查集结构存储点的关系,其中 n 为城市的个数。
方法四:Prim 算法
思路
Kruskal 算法的核心思想是每次把权重最小的边加入到树中,Prim 算法则是依据顶点来生成的,它的每一步都会为一颗生长中的树添加一条边,一开始这棵树只有一个顶点,然后会添加 n - 1 条边,每次都是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入到树中。
算法
- 根据 connections 记录每个顶点到其他顶点的权重,记为 edges 。
- 使用 visited 记录所有被访问过的点。
- 使用堆来根据权重比较所有的边。
- 将任意一个点记为已访问,并将其所有连接的边放入堆中。
- 从堆中拿出权重最小的边。
- 如果已经访问过,直接丢弃。
- 如果未访问过,标记为已访问,并且将其所有连接的边放入堆中,检查是否有 n 个点。
重复操作 5。
1 | class Solution { |
2022. 将一维数组转变成二维数组
三种方法
遍历赋值
1 | class Solution { |
Arrays.copyOfRange
- original:第一个参数为要拷贝的数组对象
- from:第二个参数为拷贝的开始位置(包含)
- to:第三个参数为拷贝的结束位置(不包含)
1 | class Solution { |
System.arraycopy
- 第一个参数默认是src 来源数组 类型为数组
- 第二个参数默认是srcPos 从来源数组开始复制的位置 类型为整行(其实就是下标)
- 第三个参数默认是dest 目标数组 类型为数组
- 第四个参数默认是destPos 目标数组起始下标
- 第五个参数默认是length 复制的长度
1 | class Solution { |
1185. 一周中的第几天
method1:
1 | class Solution { |
method2:
1 | class Solution { |
34. 在排序数组中查找元素的第一个和最后一个位置
1 | class Solution { |
1576. 替换所有的问号
1 | class Solution { |
71. 简化路径
1 | class Solution { |
1614. 括号的最大嵌套深度
1 | class Solution { |
89. 格雷编码
1 | class Solution { |
1629. 按键持续时间最长的键
1 | class Solution { |
306. 累加数
1 | class Solution { |
1036. 逃离大迷宫
1 | class Solution { |
不同于普通的 DFS、BFS,因为数据范围太大,如果直接开二维数组来存matrix或是visited,会超出内存限制,而应该保存对应位置到Set中。同样的,为了不超时,应该在搜索一定的范围后剪枝,因为0 <= blocked.length <= 200,如果能搜出曼哈顿距离大于 200 的范围,则能保证出发点没有被 block 住,一定能到达。
334. 递增的三元子序列
1 | class Solution { |
747. 至少是其他数字两倍的最大数
1 | class Solution { |
373. 查找和最小的 K 对数字
1 | class Solution { |
1716. 计算力扣银行的钱
1 | class Solution { |
382. 链表随机节点
1 | class Solution { |
1220. 统计元音字母序列的数目
题目中给定的字符的下一个字符的规则如下:
- 字符串中的每个字符都应当是小写元音字母 (‘a’,‘e’,‘i’,‘o’,‘u’)
- 每个元音‘a’ 后面都只能跟着 ‘e’;
- 每个元音 ‘e’后面只能跟着 ‘a’ 或者是 ‘i’;
- 每个元音 ‘i’ 后面不能再跟着另一个 ‘i’;
- 每个元音 ‘o’后面只能跟着 ‘i’ 或者是 ‘u’;
- 每个元音 ‘u’ 后面只能跟着 ‘a’;
以上等价于每个字符的前一个字符的规则如下:
- 元音字母 ‘a’ 前面只能跟着 ‘e’,‘i’,‘u’
- 元音字母 ‘e’前面只能跟着 ‘a’,‘i’;
- 每个元音 ‘i’ 前面只能跟着 ‘e’,‘o’
- 每个元音 ‘o’ 前面只能跟着 ‘i’
- 每个元音 ‘u’ 后面只能跟着 ‘o’,‘i’;
我们设dp[i][j]代表当前长度为i且以字符j为结尾的字符串的数目,其中j=0,1,2,3,4分别代表元音字母‘a’,‘e’,‘i’,‘o’,‘u’,通过以上的字符规则,我们可以得到动态规划递推公式如下:
统计元音字母序列的数目

- 实际计算过程中只需要保留前一个状态即可推导出后一个状态,计算长度为
i的状态只需要长度为i−1的中间变量即可,i−1之前的状态全部都可以丢弃掉。计算过程中,答案需要取模1e9+7。
1 | class Solution { |
539. 最小时间差
方法一:排序
将 timePoints排序后,最小时间差必然出现在 timePoints 的两个相邻时间,或者 timePoints的两个首尾时间中。因此排序后遍历一遍timePoints 即可得到最小时间差。
1 | class Solution { |
方法二:鸽巢原理
根据题意,一共有 24×60=1440种不同的时间。由鸽巢原理可知,如果 timePoints 的长度超过 1440,那么必然会有两个相同的时间,此时可以直接返回 0。
1 | class Solution { |
方法三
1 | class Solution { |
219. 存在重复元素 II
1 | class Solution { |
1492. n 的第 k 个因子
1 | class Solution { |
1345. 跳跃游戏 IV
1 | class Solution { |
1332. 删除回文子序列
1 | class Solution { |
2034. 股票价格波动
1 | class StockPrice { |
1688. 比赛中的配对次数
method1:数学推理:最终冠军只剩一个队伍,因此有n - 1个无法晋级的队伍,也就会有n - 1场比赛
1 | class Solution { |
method2:直接计算
1 | class Solution { |
2013. 检测正方形
1 | class DetectSquares { |
2047. 句子中的有效单词数
1 | class Solution { |
1996. 游戏中弱角色的数量
1 | class Solution { |
1765. 地图中的最高点
1 | class Solution { |
884. 两句话中的不常见单词
1 | class Solution { |
1342. 将数字变成 0 的操作次数
1 | class Solution { |
680. 回文字符串
1 | public boolean validPalindrome(String s) { |
88. 归并两个有序数组
需要从尾开始遍历,否则在 nums1 上归并得到的值会覆盖还未进行归并比较的值。
1 | public void merge(int[] nums1, int m, int[] nums2, int n) { |
630. 课程表 III
方法一:优先队列 + 贪心



1 | class Solution { |
1462. 课程表 IV
方法一:广度优先搜索 + 拓扑排序
思路与算法

1 | class Solution { |
方法二:深度优先搜索 + 拓扑排序

1 | class Solution { |
486.预测赢家

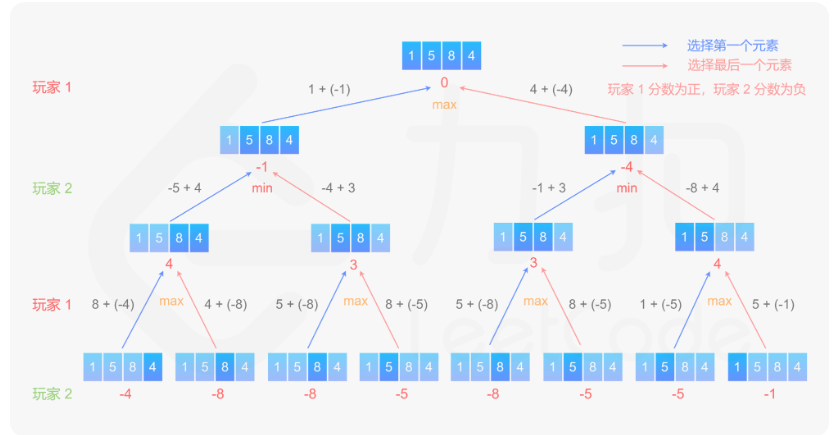
1 | class Solution { |
上述最后一行代码可改成:
1 | if(turn == 1){ |

1 | class Solution { |

1 | class Solution { |

