大厂面试智力题

大厂相关智力题。

微软面试题：红帽子与黑帽子

故事起源：

一群人开舞会，每人都戴着一顶帽子。帽子只有红和黑两种，其中黑的至少有一顶。每个人能看到其它人的帽子颜色，但看不到自己的。

大家先一起做一个游戏，规则如下：
所有人先看别人头上戴的是什么帽子，然后关灯，如果有人认为自己戴的黑帽子，就打自己一个耳光。

游戏开始：

第一次关灯，没有声音。

于是打开灯再看一遍，第二次关灯，依然鸦雀无声。
一直到第三次关灯，才有声音响起。

问：有多少人戴着黑帽子？

分析

假设有5个红帽子，和5个黑帽子。

对于红帽子的人，他看到的是有4个红帽子，和5个黑帽子。

对于黑帽子的人，他看到的是有5个红帽子，和4个黑帽子。

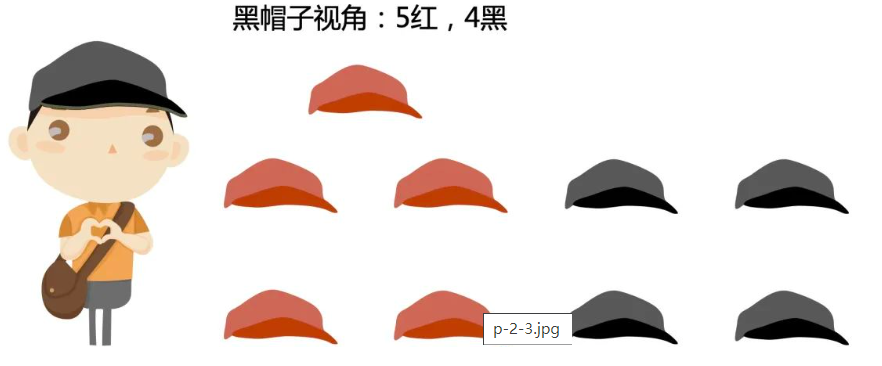
那么第一次关灯，对于任何一个人，只能得到上面的信息，他是无法判断自己的帽子颜色的，所以肯定啥也不发生。

寻找突破口

题目是问戴黑帽子的有几个人，跟具体人数相关。但我们再回到题目描述，并没有给总共多少人，也没有说红帽子有多少人，只有一个跟数字相关的条件，就是戴黑帽子的至少有一人，这就是突破口。

所以这类的问题都可以从题目的信息量上面寻找突破口。
没有说红帽子有多少人，说明解题的思路肯定跟红帽子没什么关系，有多少都无所谓，那就从黑帽子开始思考。

小规模简单场景

假设只有1个黑帽子

对于每一个红帽子，他看到的场景是这样的。第一次关灯他们都无法确定自己帽子的颜色。

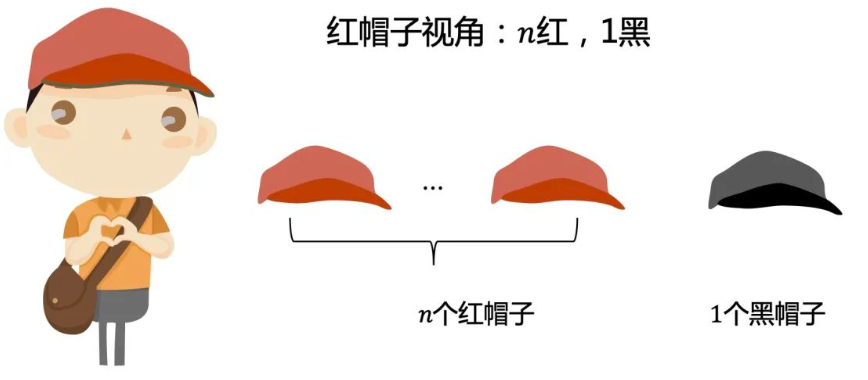
对于唯一的一个黑帽子，他看到的场景是这样的。因为至少有一个黑帽子，他没有看到，所以推出自己一定是黑帽子，第一次关灯声音响起。

假设有2个黑帽子

对于每一个红帽子，他看到的场景是这样的。第一次关灯他们是无法判断的。

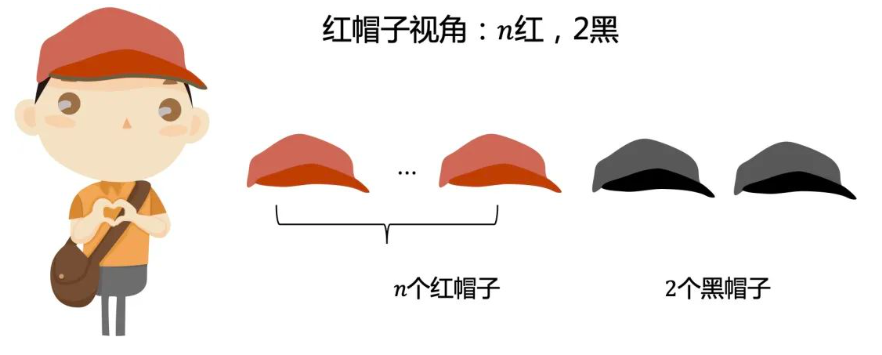
对于2个黑帽子，他看到的场景是这样的。

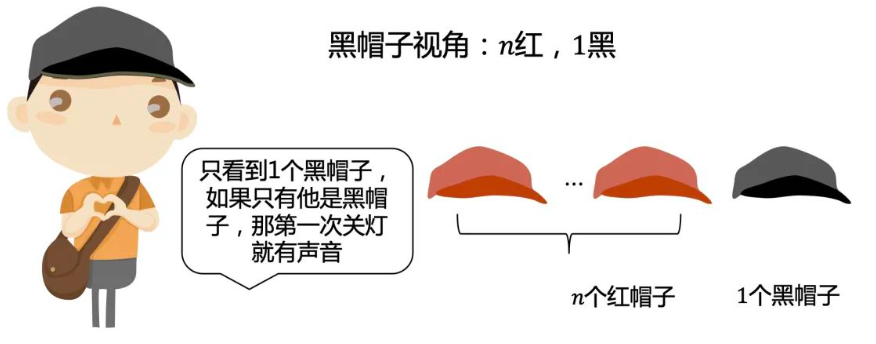
第一次关灯，他们都在等对方打耳光，所以什么也不会发生。

因为第一次没有声音，这时他俩都知道，第一次对方在等自己打耳光。所以这时他们都可以判断自己是黑帽子，第二次关灯声音响起。

假设有3个黑帽子

对于红帽子的人来说，一定比黑帽子的人后得到信息，所以不考虑。

对于其中的每一个黑帽子，他们认为2次之后对方可以发现，结果两次之后因为都在等，不会有声音，那第三次都可以判断自己是黑帽子了。

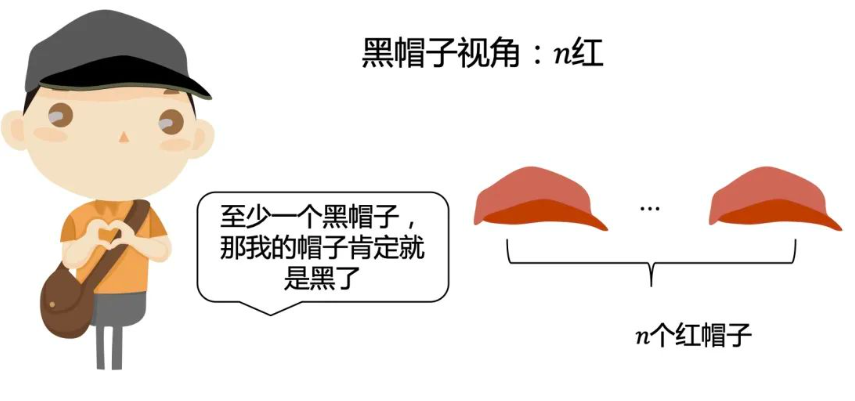
假设有N个黑帽子

根据上面分析，可以推论第N次声音响起。所以题目第3次有声音，也就意味着有3个黑帽子。

总结

对于所有的红帽子，他们的地位是相同的，也就是视角永远一样，对黑帽子也同样成立，所以如果有信息就会是同时得到，而不是一些人先发现。那这个问题就分红黑两类来考虑就行了。这也是属于博弈论相关的问题，可以先考虑小数据的简单场景。

放苹果

故事起源

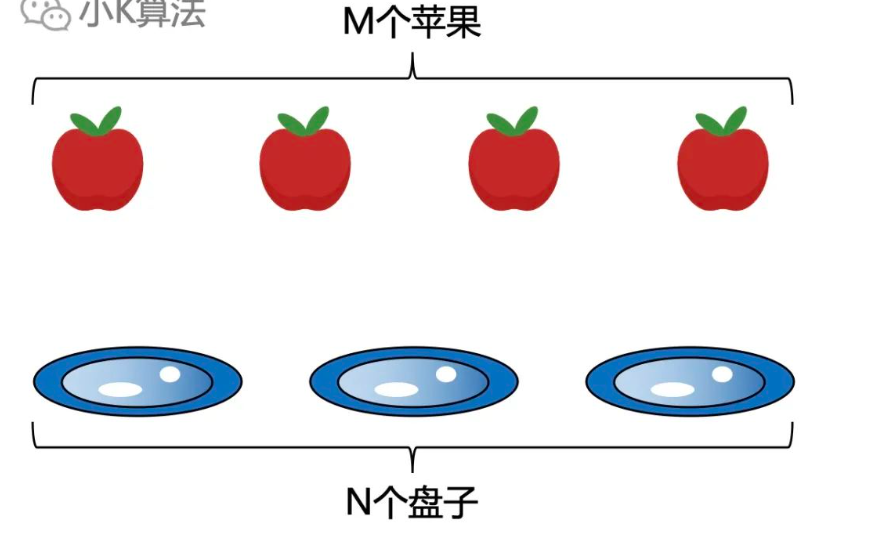
把M个苹果放在N个盘子里，允许有的盘子空着不放，那么总共有多少种不同的分法呢？
注：5，1，1和1，5，1是同一种分法，且1<=M，N<=10。

分析

苹果和盘子数量关系

苹果和盘子的数量没有说明大小关系，那就意味着有3种情况：

• 苹果比盘子多

• 苹果比盘子少

• 苹果和盘子数量相同

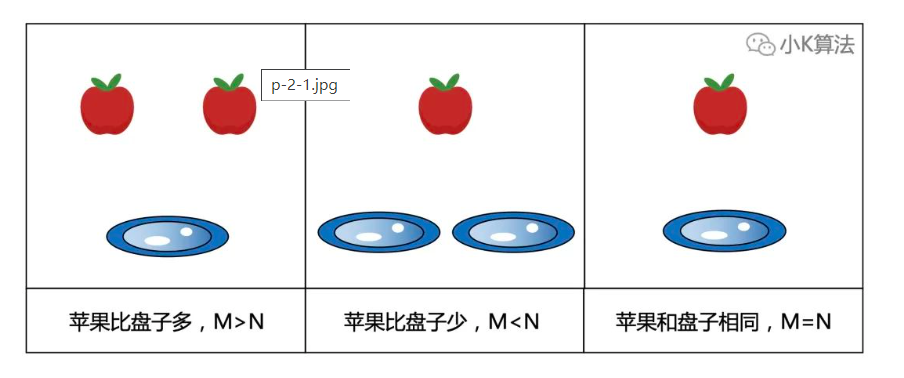
如果苹果多，那么一定会有盘子放超过一个苹果。如果盘子多，那么一定会有空盘子。如果相等，情况就不一定。

判断分法是否相同

所有的苹果是相同的，所有的盘子也是相同的，所以他们本身是无序的。
其实这个问题就是把M个苹果分成不超过N堆，总共有多少种分法。所以可先按每堆苹果数量排序，依次比较每一堆的苹果，如果所有堆都一样才是相同的分法。这也就意味着堆数肯定相同，然后排序后每一堆也相同，这样才算是相同的分法。

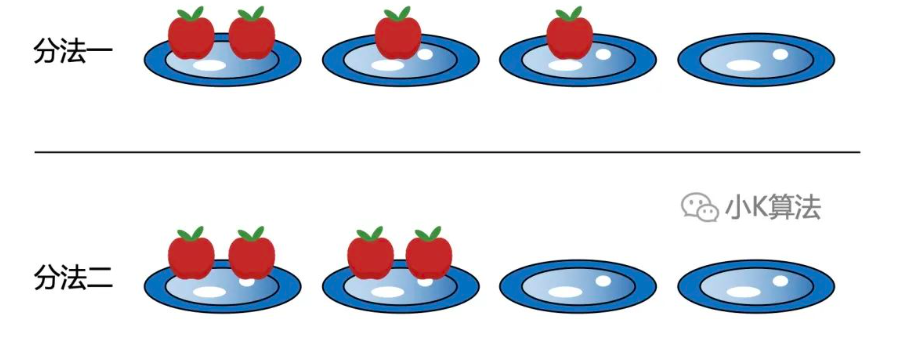
怎样才是不同分法

上面有了相同分法的判断，那取反后自然就是不同的分法了。

• 堆数不同一定是不同的分法。

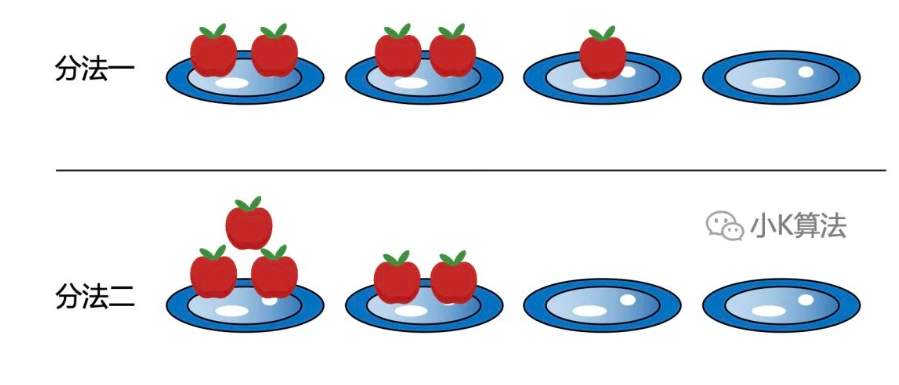
• 堆数相同，但排序后，有超过一堆的数量不相同

如下，堆数不同，所以是不同的分法。

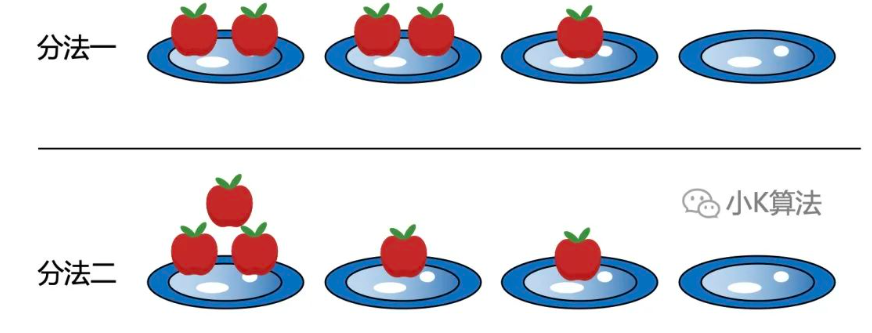
如下，堆数相同，但有超过一堆的数量不同，所以也是不同的分法。

划分子问题

知道了如何区分不同的分法，接着就是如何求出总共有多少种分法。

首先可以按堆数来划分，比如依次将M个苹果刚好分成1堆，2堆…，N堆，把所有的分法加起来，不就是总共不同的分法了吗？

设f[m,n]表示M个苹果刚好分成N堆的方法数。

那f[m,n]应该怎么求呢，或者说这个能否划分成小的子问题来求解？

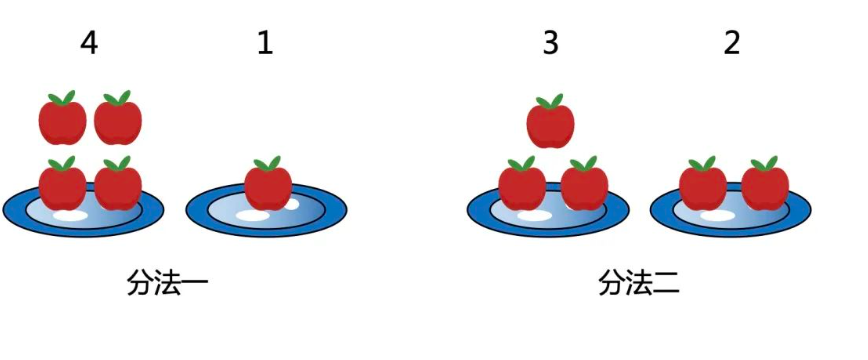
举例：

假设有5个苹果，需要刚好分成2堆，即f[5,2]。直接人工枚举，可以知道只有如下2种情况，即f[5,2]=2。

继续思考，5个苹果要分成2堆，那这两堆，每一堆至少得有1个苹果，所以可以先在每一堆中放1个苹果，剩下的是不是就可以随意划分了。

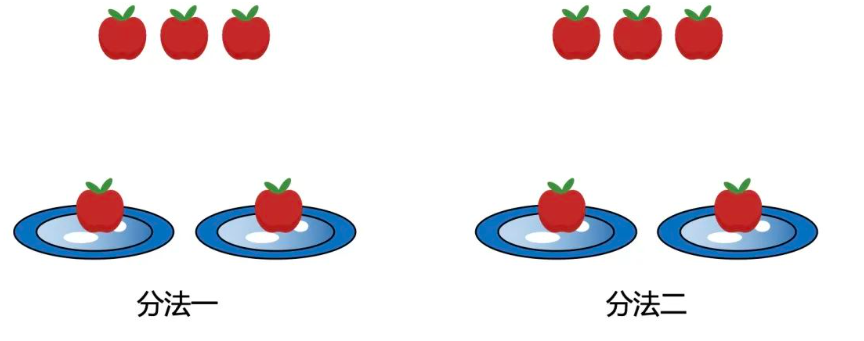
还剩下3个苹果可以随意划分，但依然不能重复，那问题是不是就变成把3个苹果分成1堆，2堆，即f[3,1],f[3,2]。

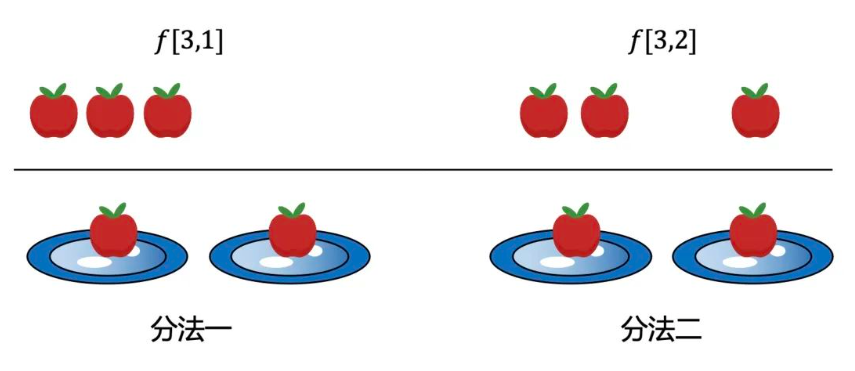
再仔细观察，这两种划分如果再合并上每一堆已经有的1个苹果，是不是和上面的f[5,2]的分法完全一样啊，这样已经划分出了子问题，接下来就依次求解就好了。

算法建模

设f[m,n]表示M个苹果刚好分成N堆的方法数，那最终要求的就是f[m,1]+f[m,2]+…+f[m,n]。

这是一个递推关系，那肯定得有边界，不然从何推起呢？

前面已经分析了m，n的大小关系不定，也就是有3种情况。

• m<n，把m个苹果刚好分成n堆，明显是不可能的，所以f[m,n]=0

• m=n，把m个苹果刚好分成m堆，明显只有一种情况，就是每一堆1个，所以f[m,n]=1

• m>n，第3小节已经说明，这种情况就划分成子问题，先在每一堆放1个，剩下的再依次分成1堆，2堆…n堆，所以f[m,n]=f[m-n,1]+f[m-n,2]+…+f[m-n,n]

代码实现

变量定义

int f[11][11];

递归子问题

int solve(int m, int n) {
    if (f[m][n] != -1) return f[m][n];
    if (m < n) {
        f[m][n] = 0;
        return f[m][n];
    }
    if (m == n || n == 1) {
        f[m][n] = 1;
        return f[m][n];
    }
    f[m][n] = 0;
    for (int i = 1; i <= n; ++i) {
        f[m][n] += solve(m - n, i);
    }
    return f[m][n];
}

main

int main() {
    int n, m;
    // 初始化为-1
    memset(f, 0xff, sizeof(f));
    cin >> m >> n;
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        ans += solve(m, i);
    }
    cout << ans << endl;
    return 0;
}

番外篇

以为已经解决完了？其实还没结束呢，因为还有一个更高级的解法，不过抽象程度更高，不太好理解。

把M个苹果放在N个盘子里，其实可以直接划分成两种情况：

• 有空盘子

• 没有空盘子

那结果就是把两种情况相加即可。

那怎么分解子问题呢，其实还是一样的，子问题也包括有空盘子和没有空盘子。

还是假设M个苹果，N个盘子。

有空盘子如何分解：

其实就是先拿一个盘子出来空着，这样就变成了M个苹果，N-1个盘子。

没有空盘子如何分解：

其实就是先在每一个盘子放一个，这样就变成了M-N个苹果，N个盘子。

我猜肯定有人会问，这样会不会重复统计啊。其实不会，上面2种大的情况肯定不会重复，在分解子问题的时候，子问题的属性并不会变。比如左边蓝色已经有一个空盘，下面的子问题无论怎么放置都有空盘。同理右边红色因为最开始已经在每个盘子放了一个苹果，所以无论子问题怎么放也一定没有空盘。

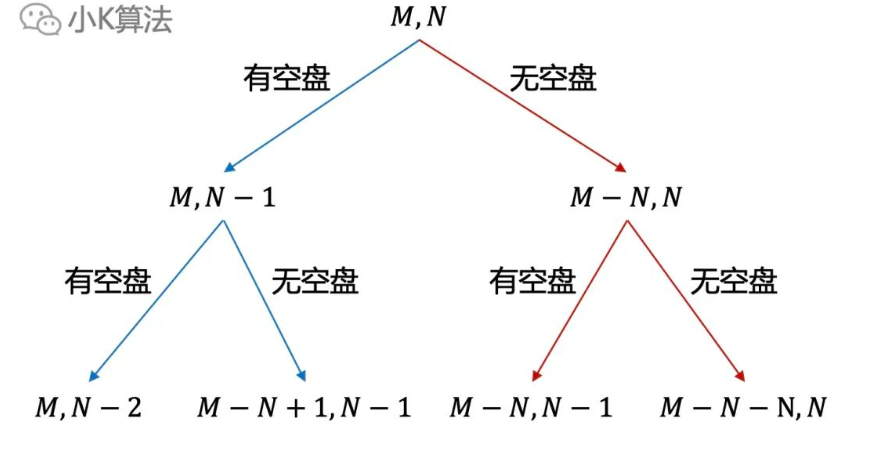
递归子问题分解出来的情况不会有重复，那组合起来也肯定不会有重复，所以这样递归出来的就是所有不同分法了。

而且每下分一次，一种是苹果减少，一种是空盘增多，因为总盘子数不变，那也就意味着有苹果的盘子数减少，即堆数减少，这不就是之前根据堆数不同的划分方法吗？苹果减少对应分解子问题，堆数减少对应分类，我们似乎在两种不同的方法间找到了一种莫名的联系。

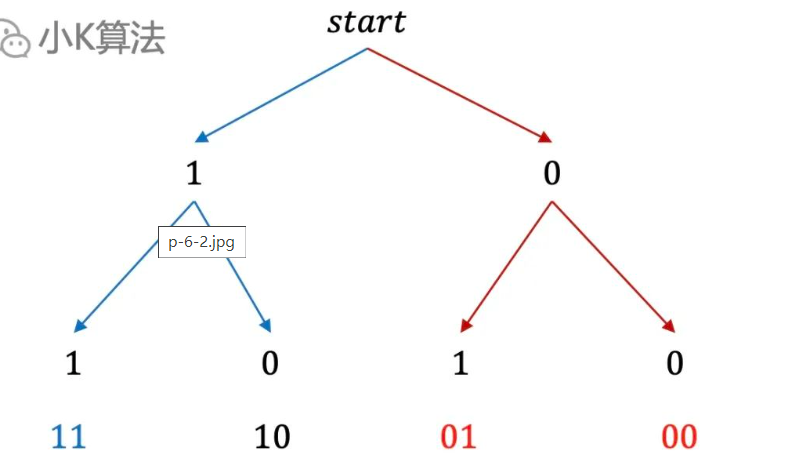
再画一个更形象的图帮大家理解，假设我要用0和1组合成不同的二进制数，从首位开始划分以0开头和以1开头，递归子问题依然保持这种性质，那么最终得到的数肯定不会有重复的。这跟上面的场景虽然不同，但都有类似的思想。

代码实现

int solve(int m, int n) {
    if (m < 0) return 0;
    if (m == 0 || n == 1) return 1;
    return solve(m - n, n) + solve(m, n - 1);
}

整数划分

再继续把问题抽象一下，如下有一个这样的数学问题：
把一个整数n写成多个大于等于1小于等于它本身的整数的和，即n=m1+m2+…，则[m1,m2…]构成的一个集合称为n的一个划分，那么总共有多少种不同的划分呢？
你品，你细品，这不就是同一个问题吗，只不过我们把它抽象成了一个纯数学问题，这就是很经典的整数划分问题。

总结

一般求总数的问题有几种情况，一是用排列组合公式，二是套用某种数列，如斐波拉契数列，三是自己构建递推或者递归公式。这个题首先可能会想到排列组合，高中数学经常遇到类似的问题，经典解法是“隔板法”。但这个问题的元素都是相同的，也无序，最大的难点就在于如何去重，所以排列组合不好解。不能直接套公式，那就用递推的方式分解子问题，其它就交给代码就好了。

整个代码实现还是比较简单，但思考的过程其实并不简单，抽象思维的地方会比较多，大家要多分析规律，把抽象的问题变成具象的过程，这样就容易多了.